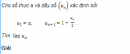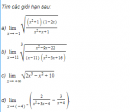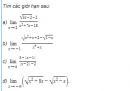Câu 4.74 trang 148 sách bài tập Đại số và Giải tích 11 Nâng caoCho dãy số xác định bởi Cho dãy số \(\left( {{u_n}} \right)\) xác định bởi \(\left\{ \matrix{ Trong đó \( - 1 < a < 0.\) a) Chứng minh rằng \( - 1 < {u_n} < 0.\) với mọi n và \(\left( {{u_n}} \right)\) là một dãy số giảm. b) Chứng minh rằng \( - 1 < {u_{n + 1}} + 1 \le {1 \over {\sqrt {{a^2} + 1} }}\left( {{u_n} + 1} \right)\) với mọi n. c) Tìm \(\mathop {\lim }\limits_{x \to \infty } {u_n}.\) Giải a) Ta chứng minh bằng phương pháp quy nạp. Theo giả thiết, điều khẳng định đúng với \(n = 1.\) Giả sử điều khẳng định đúng với n , tức là \( - 1 < {u_n} < 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(2)\) Ta chứng minh nó đúng với \(n + 1.\) Thật vậy, từ (2) suy ra \(0 < {u_{n + 1}} + 1 < 1\,;\,\) Do đó \(0 < {{{u_n} + 1} \over {\sqrt {u_n^2 + 1} }} < 1\) Và \( - 1 < {{{u_n} + 1} \over {\sqrt {u_n^2 + 1} }} - 1 < 0,\) Tức là \( - 1 < {u_{n + 1}} < 0.\,\) Vì \( - 1 < {u_n} < 0\) nên \({u_{n }} +1> 0\) và \(u_n^2 > 0\) với mọi n . Do đó từ (1) suy ra \({u_{n + 1}} < \left( {{u_n} + 1} \right) - 1 = {u_n}\) với mọi n. Vậy \(\left( {{u_n}} \right)\) là một dãy số giảm. b) Từ đẳng thức (1) suy ra \({u_{n + 1}} + 1 = {1 \over {\sqrt {u_n^2 + 1} }}\left( {{u_n} + 1} \right)\) với mọi n. Từ đó suy ra \(\left| {{u_n}} \right| \ge \left| a \right| \Leftrightarrow u_n^2 \ge {a^2};\) Do đó \({1 \over {\sqrt {u_n^2 + 1} }} \le {1 \over {\sqrt {{a^2} + 1} }}\) với mọi n Và từ (3), ta có \({u_{n + 1}} + 1 \le {1 \over {\sqrt {{a^2} + 1} }}\left( {{u_n} + 1} \right)\) với mọi n. Đặt \({v_n} = {u_n} + 1\) và \(q = {1 \over {\sqrt {{a^2} + 1} }},\) ta có \(0 < q < 1,{v_n} > 0\) và \({v_{n + 1}} \le q{v_n}\) với mọi n. Từ đó ta có \(\eqalign{ Với mọi n . Vì \(\lim \left( {a + 1} \right).{q^{n - 1}} = \left( {a + 1} \right)\lim {q^{n - 1}} = 0\) nên từ đó suy ra \(\lim {v_n} = 0\) và \(\lim {u_n} = - 1.\) sachbaitap.com
Xem lời giải SGK - Toán 11 Nâng cao - Xem ngay >> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
Xem thêm tại đây:
Ôn tập chương IV - Giới hạn - SBT Toán 11 Nâng cao
|
-
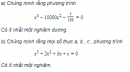
Câu 4.78 trang 149 sách bài tập Đại số và Giải tích 11 Nâng cao
Chứng minh rằng phương trình có ít nhất một nghiệm dương.

 Tải ngay
Tải ngay