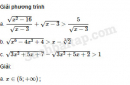Câu 4.95 trang 118 SBT Đại số 10 Nâng caoGiải bài tập Câu 4.95 trang 118 SBT Đại số 10 Nâng cao Tìm các giá trị của x thỏa mãn hệ bất phương trình : a. \(\left\{ {\begin{array}{*{20}{c}}{2{x^2} + 9x + 9 > 0}\\{5{x^2} - 7x - 3 \le 0}\end{array}} \right.\) b. \(\left\{ {\begin{array}{*{20}{c}}{3{x^2} + 11x - 4 \le 0}\\{{x^2} - 8x - 20 \le 0}\end{array}} \right.\) c. \(\left\{ {\begin{array}{*{20}{c}}{2\left( {x - 1} \right) - 3\left( {x - 4} \right) > x + 5}\\{\dfrac{{3x - 4}}{{{x^2} + 4x + 4}} \ge 0}\end{array}} \right.\) d. \(\left\{ {\begin{array}{*{20}{c}}{\dfrac{{3{x^2} - 7x + 8}}{{{x^2} + 1}} > 1}\\{\dfrac{{3{x^2} - 7x + 8}}{{{x^2} + 1}} \le 2.}\end{array}} \right.\) Giải: a. \(x \in \left[ {\dfrac{{7 - \sqrt {109} }}{{10}};\dfrac{{7 + \sqrt {109} }}{{10}}} \right];\) b. \(x \in \left[ { - 2;\dfrac{1}{3}} \right]\) c. \(x \in \left[ {\dfrac{4}{3};\dfrac{5}{2}} \right)\) d. \(x \in \left[ {1;6} \right]\) Sachbaitap.com
Xem thêm tại đây:
Bài tập Ôn tập chương IV - Bất đẳng thức và bất phương trình
|

 Tải ngay
Tải ngay