Tải ngay
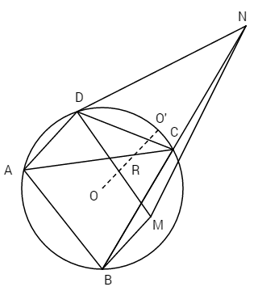
Câu 5 trang 6 Sách bài tập Hình Học 11 nâng cao.Chứng minh rằng tâm đường tròn ngoại tiếp tam giác DNM nằm trên (O; R). 5. Trang 6 Sách bài tập Hình Học 11 nâng cao. Cho tứ giác ABCD nội tiếp đường tròn (O; R) trong đó AD = R. Dựng các hình bình hành DABM và DACN. Chứng minh rằng tâm đường tròn ngoại tiếp tam giác DNM nằm trên (O; R). Giải Theo giả thiết ta có: \(\overrightarrow {AD} = \overrightarrow {BM} = \overrightarrow {CN} \) Vì vậy, phép tịnh tiến theo vecto \(\overrightarrow {AD} \) biến tam giác ABC thành tam giác DMN. Suy ra, nếu O’ là tâm đường tròn ngoại tiếp tam giác DMN thì phép tịnh tiến đó biến O thành O’, tức là: \(\overrightarrow {OO'} = \overrightarrow {AD} \) Do đó: OO' = AD = R Và vì vậy O’ nằm trên (O; R).
sachbaitap.com
Xem lời giải SGK - Toán 11 Nâng cao - Xem ngay >> Học trực tuyến Lớp 11 cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng. Cam kết giúp học sinh lớp 11 học tốt, hoàn trả học phí nếu học không hiệu quả.
Xem thêm tại đây:
Bài 1, 2: Mở đầu về phép biến hình. Phép tịnh tiến và phép dời hình
|
-
Câu 7 trang 6 Sách bài tập Hình Học 11 nâng cao.
Viết phương trình ảnh của mỗi đường thẳng sau đây qua phép tịnh tiến T.
-
Câu 8 trang 6 Sách bài tập Hình Học 11 nâng cao.
Trong mặt phẳng tọa độ Oxy cho hai đường thẳng d và d’
-
Câu 9 trang 6 Sách bài tập Hình Học 11 nâng cao.
Cho ba điểm không thẳng hàng A, B, C. Chứng tỏ rằng phép dời hình biến mỗi điểm A, B, C thành chính nó phải là phép đồng nhất.
