Tải ngay
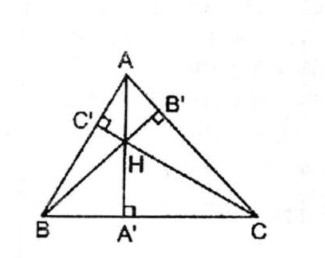
Câu 51 trang 166 Sách bài tập (SBT) Toán 8 tập 1Cho tam giác ABC với ba đường cao AA’, BB’, CC’. Gọi H là trực tâm của tam giác đó. Cho tam giác ABC với ba đường cao AA’, BB’, CC’. Gọi H là trực tâm của tam giác đó. Chứng minh rằng \({{HA'} \over {AA'}} + {{HB'} \over {BB'}} + {{HC'} \over {CC'}} = 1\) Giải:
\(\eqalign{ & {S_{HBC}} + {S_{HAC}} + {S_{HAB}} = {S_{ABC}} \cr & \Rightarrow {{{S_{HBC}}} \over {{S_{ABC}}}} + {{{S_{HABC}}} \over {{S_{ABC}}}} + {{{S_{HAB}}} \over {{S_{ABC}}}} = 1 \cr} \) Suy ra: \({{HA'.BC} \over {AA'.BC}} + {{HB'.AC} \over {BB'.AC}} + {{HC'.AB} \over {CC'.AB}} = 1\) \( \Rightarrow {{HA'} \over {AA'}} + {{HB'} \over {BB'}} + {{HC'} \over {CC'}} = 1\)
Xem lời giải SGK - Toán 8 - Xem ngay >> Học trực tuyến lớp 8 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều). Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả.
Xem thêm tại đây:
Ôn tập chương II - Đa giác - Diện tích đa giác
|
-
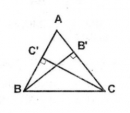
Câu 52 trang 166 Sách bài tập (SBT) Toán 8 tập 1
Cho tam giác ABC a. Tính tỉ số các đường cao BB’ và CC’ xuất phát từ các đỉnh B và C b. Tại sao nếu AB < AC thì BB’ < CC’ ?
-
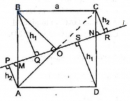
Câu 53 trang 166 Sách bài tập (SBT) Toán 8 tập 1
Hãy tính tổng các khoảng cách từ các đỉnh của hình vuông đến đường thẳng l theo a và b (a và b có cùng đơn vị đo)
-
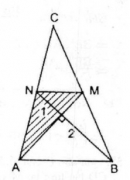
Câu 54 trang 166 Sách bài tập (SBT) Toán 8 tập 1
Tam giác ABC có hai trung tuyến AM và BN vuông góc với nhau. Hãy tính diện tích tam giác đó theo AM và BN
-
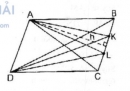
Câu 55 trang 166 Sách bài tập (SBT) Toán 8 tập 1
Cho hình bình hành ABCD. Gọi K và L là hai điểm thuộc cạnh BC sao cho BK = KL = LC. Tính tỉ số diện tích của : a. Các tam giác DAC và DCK b. Tam giác DAC và tứ giác ADLB c. Các tứ giác ABKD và ABLD
