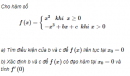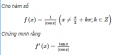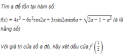Tải ngay
Câu 5.40 trang 186 sách bài tập Đại số và Giải tích 11 Nâng caoChứng minh Cho biết \(\mathop {\lim }\limits_{x \to 0} {{f\left( x \right)} \over x} = A\) và \(f\left( 0 \right) = 0.\) Chứng minh rằng \(A = f'\left( 0 \right).\) Giải Theo định nghĩa, ta có \(f'\left( 0 \right) = \mathop {\lim }\limits_{x \to 0} {{f\left( x \right) - f\left( 0 \right)} \over {x - 0}}\) Vì \(f\left( 0 \right) = 0\) nên \(f'\left( 0 \right) = \mathop {\lim }\limits_{x \to 0} {{f\left( x \right)} \over x} = A\) Sachbaitap.com
Xem lời giải SGK - Toán 11 Nâng cao - Xem ngay >> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
Xem thêm tại đây:
Ôn tập chương V - Đạo hàm
|
-
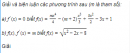
Câu 5.42 trang 186 sách bài tập Đại số và Giải tích 11 Nâng cao
Giải và biện luận các phương trình sau (m là tham số):
