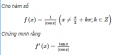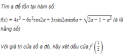Câu 5.42 trang 186 sách bài tập Đại số và Giải tích 11 Nâng caoGiải và biện luận các phương trình sau (m là tham số): Giải và biện luận các phương trình sau (m là tham số): a) \(f'\left( x \right) = 0\) biết \(f\left( x \right) = {{m{x^4}} \over 4} - \left( {m + 2} \right){{{x^3}} \over 3} + {{5{x^2}} \over 2} - 3x + 1\) b) \(f\left( x \right).f'\left( x \right) = m\) biết \(f\left( x \right) = \sqrt {{x^2} - 2x - 8} \) Giải a) Với mọi \(x \in R\), ta có \(\eqalign{& f'\left( x \right) = m{x^3} - \left( {m + 2} \right){x^2} + 5x - 3 \cr& f'\left( x \right) = 0 \Leftrightarrow m{x^3} - \left( {m + 2} \right){x^2} + 5x-3=0\,\,\,\left( 1 \right) \cr} \) Thử thấy \(x = 1\) là một nghiệm, nên ta có thể viết (1) dưới dạng \(\eqalign{& \left( {x - 1} \right)\left( {m{x^2} - 2x + 3} \right) = 0 \cr& \Leftrightarrow \left[ \matrix{x=1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {2a} \right) \hfill \cr m{x^2} - 2x + 3 = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {2b} \right) \hfill \cr} \right. \cr} \) Ta hãy giải phương trình (2b). Xét hai trường hợp \( \bullet \) Với \(m = 0\) thì \(\left( {2b} \right) \Leftrightarrow x = {3 \over 2}\) \( \bullet \) Với \(m \ne 0\) thì \(\left( {2b} \right) \Leftrightarrow x = {{1 \pm \sqrt {1 - 3m} } \over m}\) (Với điều kiện \(0 \ne m \le {1 \over 3}\) ) Kết luận + Với \(m > {1 \over 3}\), phương trình có nghiệm \({x_0} = 1\) + Với \(m = 0\), phương trình có nghiệm \({x_0} = 1\) và \({x_1} = {3 \over 2}\) + Với \(0 \ne m \le {1 \over 3}\), phương trình có các nghiệm là \({x_0} = 1,{x_1} = {{1 - \sqrt {1 - 3m} } \over m}\) và \({x_2} = {{1 + \sqrt {1 - 3m} } \over m}\) b) Để hàm số đã cho cá đạo hàm thì ta phải có \({x^2} - 2x - 8 > 0 \Leftrightarrow x < - 2\) hoặc \(x > 4.\) Với điều kiện \(x < - 2\) hoặc \(x > 4,\) ta có \(f'\left( x \right) = {{x - 1} \over {\sqrt {{x^2} - 2x - 8} }}\) Phương trình \(\eqalign{& f\left( x \right).f'\left( x \right) = m\cr& \Leftrightarrow \left\{ \matrix{x < - 2\text{ hoặc }x > 4 \hfill \cr{{x - 1} \over {\sqrt {{x^2} - 2x - 8} }}.\sqrt {{x^2} - 2x - 8} = m \hfill \cr} \right.\cr& \Leftrightarrow \left\{\matrix{x < - 2\text{ hoặc }x > 4 \hfill \cr x - 1 = m \hfill \cr} \right. \cr& \Leftrightarrow \left[ \matrix{\left\{ \matrix{x = 1 + m \hfill \cr1 + m < - 2 \hfill \cr} \right. \hfill \cr\left\{ \matrix{x = 1 + m \hfill \cr1 + m > 4 \hfill \cr} \right. \hfill \cr} \right.\cr& \Leftrightarrow \left[ \matrix{\left\{ \matrix{x = 1 + m \hfill \cr m < - 3 \hfill \cr} \right. \hfill \cr\left\{ \matrix{x = 1 + m \hfill \cr m > 3 \hfill \cr} \right. \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{x = 1 + m \hfill \cr\left| m \right| > 3 \hfill \cr} \right. \cr} \) Kết luận + Với \(\left| m \right| \le 3\) thì phương trình đã cho vô nghiệm. + Với \(\left| m \right| > 3\) thì phương trình đã cho có nghiệm là \(x = 1 + m.\) Sachbaitap.com
Xem lời giải SGK - Toán 11 Nâng cao - Xem ngay >> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
Xem thêm tại đây:
Ôn tập chương V - Đạo hàm
|
-
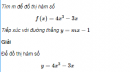
Câu 5.45 trang 186 sách bài tập Đại số và Giải tích 11 Nâng cao
Tìm m để đồ thị hàm số tiếp xúc với đường thẳng
-

Câu 5.46 trang 186 sách bài tập Đại số và Giải tích 11 Nâng cao
Cho hàm số, viết phương trình tiếp tuyến của đồ thị hai hàm số đã cho tại giao điểm của chúng. Tính góc giữa hai tiếp tuyến kể trên.

 Tải ngay
Tải ngay