Câu 5.47 trang 186 sách bài tập Đại số và Giải tích 11 Nâng caoMột đoàn tàu hỏa rời ga, chuyển động nhanh dần đều Một đoàn tàu hỏa rời ga, chuyển động nhanh dần đều với gia tốc \(0,1\,\,m/{s^2}\) (bỏ qua sức cản của không khí). Tính vận tốc tức thời tại thời điểm tàu đã đi được đúng 500m Giải Nếu chọn trục \(Os\) trùng với phương của chuyển động và chiều dương là chiều chuyển động, gốc O là vị trí ban đầu trước khi tàu khởi hành và xem \(t = 0\) là thời điểm tàu bắt đầu khởi hành, thế thì phương trình chuyển động của đoàn tàu là \(s = {1 \over 2}a{t^2} = {1 \over 2}.(0,1){t^2}\) (s là quãng đường đi được, a là gia tốc) . Gọi \({t_0}\left( {{t_0} > 0} \right)\) là khoảng thời gian từ lúc đoàn tàu rời ga đến khi đi được 500m, ta có \(500 = {1 \over 2}.\left( {0,1} \right)t_0^2 \Leftrightarrow {t_0} = 100\left( s \right)\) Vậy vận tốc tức thời tại thời điểm tàu đã đi được bằng đúng 500m là \(v\left( {{t_0}} \right) = v\left( {100} \right) = 0,1 \times 100 = 10\,\,\,\left( {m/s} \right)\) Sachbaitap.com
Xem lời giải SGK - Toán 11 Nâng cao - Xem ngay >> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
Xem thêm tại đây:
Ôn tập chương V - Đạo hàm
|
-
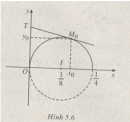
Câu 5.50 trang 187 sách bài tập Đại số và Giải tích 11 Nâng cao
Chứng minh rằng tiếp tuyến tại điểm bất kì của đồ thị hàm số, cắt trục tung tại một điểm cách đều tiếp điểm và gốc tọa độ.
-
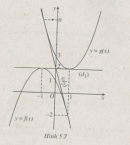
Câu 5.51 trang 187 sách bài tập Đại số và Giải tích 11 Nâng cao
Gọi (P) và (P’) lần lượt là đồ thị của hai hàm số a) Vẽ các đồ thị của hai hàm số đó trên cùng một hệ trục tọa độ. b) Viết phương trình của đường thẳng (d) là tiếp tuyến của (P) để tiếp điểm A đồng thời cũng là tiếp tuyến của (P’) tại tiếp điểm B (đường thẳng (d) nếu có, được gọi là tiếp tuyến chung của (P) và (P’).

 Tải ngay
Tải ngay