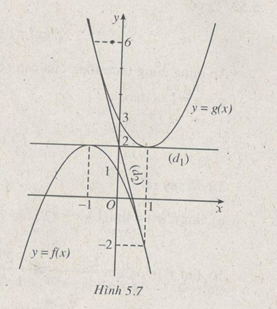
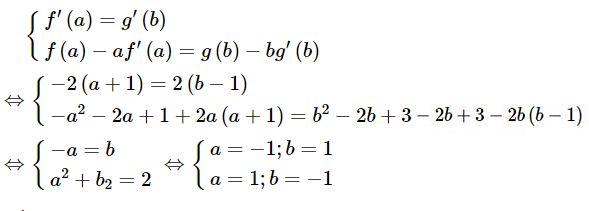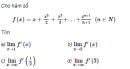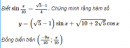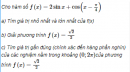Câu 5.51 trang 187 sách bài tập Đại số và Giải tích 11 Nâng cao

Gọi (P) và (P’) lần lượt là đồ thị của hai hàm số

a) Vẽ các đồ thị của hai hàm số đó trên cùng một hệ trục tọa độ.

b) Viết phương trình của đường thẳng (d) là tiếp tuyến của (P) để tiếp điểm A đồng thời cũng là tiếp tuyến của (P’) tại tiếp điểm B (đường thẳng (d) nếu có, được gọi là tiếp tuyến chung của  (P) và (P’).

Giải

a)

b) Gọi đường thẳng \(y = mx + p\,\,\,\left( d \right)\) là tiếp tuyến của đồ thị hàm số \(y = f\left( x \right) =  - {x^2} - 2x + 1\) tại điểm \(A\left( {a;f\left( a \right)} \right),\) đồng thời là tiếp tuyến của đồ thị hàm số \(y = g\left( x \right) = {x^2} - 2x + 3\) tại điểm \(B\left( {b;g\left( b \right)} \right).\) Nếu thế thì ta phải có

\(\left( I \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left\{ \matrix{ f'\left( a \right) = g'\left( b \right) = m\,\,\,\,\,\left( 1 \right) \hfill \cr f\left( a \right) = ma + p\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right) \hfill \cr g\left( b \right) = mb + p\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 3 \right) \hfill \cr}  \right.\)

((I) chứng tỏ hệ số góc của tiếp tuyến tại A (đối với (P) và hệ số góc của tiếp tuyến B (đối với (P’)) bằng nhau và bằng m; (2) chứng tỏ đường thẳng (d) đi  qua đoạn A; (3) chứng tỏ đường thẳng (d) đi qua B)

Khử m và p ở hệ phương trình (1), ta được

Thế vào (1) ta được

- Với \(a =  - 1;b = 1\) thì \(m = 0\) và \(p = 2,\) suy ra tiếp tuyến chung phải tìm là \(y = 2\left( {{d_1}} \right)\)

- Với \(a = 1;b =  - 1\) thì \(m =  - 4\) và \(p = 2,\) suy ra tiếp tuyến chung phải tìm là \(y =  - 4x + 2\left( {{d_2}} \right)\)

Sachbaitap.com