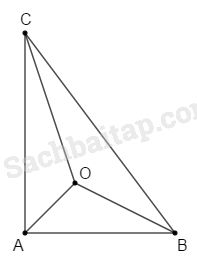
Câu 6.1, 6.2, 6.3, 6.4 trang 47 Sách Bài Tập (SBT) Toán lớp 7 tập 2Khẳng định nào sau đây sai? Câu 6.1 trang 47 Sách Bài Tập (SBT) Toán lớp 7 tập 2 Cho tam giác ABC. Trên tia phân giác của góc B, lấy điểm O nằm trong tam giác ABC sao cho O cách đều hai cạnh AB, AC. Khẳng định nào sau đây sai? (A) Điểm O nằm trên tia phân giác của góc A. (B) Điểm O không nằm trên tia phân giác của góc C. (C) Điểm O cách đều AB, BC. (D) Điểm O cách đều AB, AC, BC. Giải Điểm O cách đều AB, AC nên O thuộc tia phân giác của góc A. Mặt khác, O thuộc tia phân giác của góc B nên O là giao điểm của ba đường phân giác của tam giác ABC. Vậy (B) sai còn (A), (C), (D) đúng. Đáp số: (B) Điểm O không nằm trên tia phân giác của góc C. Câu 6.2 trang 47 Sách Bài Tập (SBT) Toán lớp 7 tập 2 Cho tam giác ABC có \(\widehat A = \widehat B + \widehat C\). Hai đường phân giác của góc A và góc C cắt nhau tại O. Khi đó BOC bằng: (A) 85° ; (B) 90° ; (C) 135° ; (D) 150° Giải
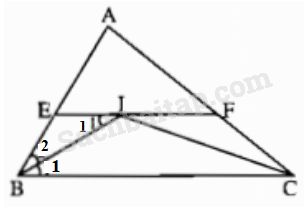
Tam giác ABC có \(\widehat A = \widehat B + \widehat C\) vuông tại A ; AO, CO lần lượt là tia phân giác của \(\widehat A\) và \(\widehat C\) nên BO là tia phân giác của \(\widehat B\). Ta có \(\widehat {OBC} + \widehat {OCB} = {1 \over 2}\left( {\widehat B + \widehat C} \right) = 45^\circ \) nên \(\widehat {BOC} = 180^o-45^o=135^\circ \) Chọn (C) 135°. Câu 6.3 trang 47 Sách Bài Tập (SBT) Toán lớp 7 tập 2 Cho tam giác ABC. Gọi I là điểm nằm trong tam giác và cách đều ba cạnh của tam giác đó. Qua I kẻ đường thẳng song song với BC cắt AB, AC lần lượt tại E và F. Chứng minh rằng EF = BE + CF. Giải
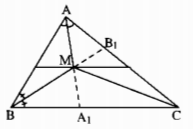
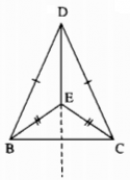
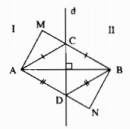
Vì điểm I cách đều ba cạnh của tam giác ABC và nằm trong tam giác nên I là giao điểm của ba đường phân giác của tam giác ABC, tức là BI, CI lần lượt là tia phân giác của góc B và góc C. Do EF // BC nên \(\widehat {{B_1}} = \widehat {{I_1}}\)(so le trong), suy ra \(\widehat {{I_1}} = \widehat {{B_2}}\). Vậy tam giác EBI cân tại E, tức là EI = EB. Tương tự ta có FI = FC Vậy EF = EI + IF = BE = CF. Câu 6.4 trang 47 Sách Bài Tập (SBT) Toán lớp 7 tập 2 Hai đường phân giác \({\rm{A}}{{\rm{A}}_1}\) và \(B{B_1}\) của tam giác ABC cắt nhau tại M. Hãy tìm các góc ACM, BCM nếu \({\rm{a}})\widehat {AMB} = 136^\circ \) \(b)\widehat {AMB = }111^\circ \) Giải
Do ba đường phân giác của một tam giác đồng quy tại một điểm nên CM là tia phân giác của góc C. a) \({1 \over 2}\left( {\widehat A + \widehat B} \right) = \widehat {MAB} + \widehat {MBA} = 180 - \widehat {AMB}\) \( = 180^\circ - 136^\circ = 44^\circ \) Suy ra \(\widehat A + \widehat B = 2.44^\circ = 88^\circ \) \(\widehat C = 180^\circ - 88^\circ = 92^\circ \) Vậy \(\widehat {ACM} = \widehat {BCM} = 92^\circ :2^\circ = 46^\circ \) b) Ta có \({1 \over 2}\left( {\widehat A + \widehat B} \right) = 180^\circ - 111^\circ = 69^\circ \). Suy ra \(\widehat A + \widehat B = 138^\circ \) Suy ra \(\widehat C = 180^\circ - 138^\circ = 42^\circ \). Vậy \(\widehat {ACM} = \widehat {BCM} = 21^\circ \). Sachbaitap.com
Xem lời giải SGK - Toán 7 - Xem ngay >> Học trực tuyến lớp 7 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 7 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
Xem thêm tại đây:
Bài 6: Tính chất ba đường phân giác của tam giác
|
-
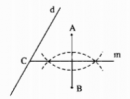
Câu 56 trang 47 Sách Bài Tập (SBT) Toán lớp 7 tập 2
Tìm một điểm C nằm trên d sao cho C cách đều A và B.

 Tải ngay
Tải ngay