Tải ngay
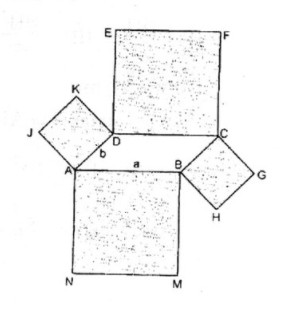
Câu 6.2 trang 165 Sách bài tập (SBT) Toán 8 tập 1Tính theo a, b và S diện tích của đa giác giới hạn bởi các cạnh của hình vuông mà không là cạnh của hình bình hành đã cho. Cho hình bình hành ABCD, với diện tích S và AB = a, AD = b. Lấy mỗi cạnh của hình bình hành đó làm cạnh dựng một hình vuông ra phía ngoài hình bình hành. Tính theo a, b và S diện tích của đa giác giới hạn bởi các cạnh của hình vuông mà không là cạnh của hình bình hành đã cho. Giải:
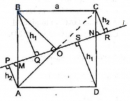
Hình đa giác đó gồm hình bình hành ABCD, hình vuông ABMN, BHGC, CFED, DKJA. \(\eqalign{ & {S_{ABMN}} = {S_{CDEF}} = {a^2} \cr & {S_{BHGC}} = {S_{DKJA}} = {b^2} \cr} \) Diện tích đa giác bằng : \(\eqalign{ & {S_{ABMN}} = {S_{CDEF}} = {a^2} \cr & {S_{BHGC}} = {S_{DKJA}} = {b^2} \cr} \)
Xem lời giải SGK - Toán 8 - Xem ngay >> Học trực tuyến lớp 8 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều). Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả.
Xem thêm tại đây:
Bài 6. Diện tích đa giác
|
-
Câu 6.3 trang 165 Sách bài tập (SBT) Toán 8 tập 1
Bạn Giang đã vẽ một đa giác ABCDEFGHI như ở hình bs. 26.
-
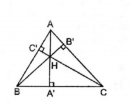
Câu 51 trang 166 Sách bài tập (SBT) Toán 8 tập 1
Cho tam giác ABC với ba đường cao AA’, BB’, CC’. Gọi H là trực tâm của tam giác đó.
-
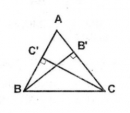
Câu 52 trang 166 Sách bài tập (SBT) Toán 8 tập 1
Cho tam giác ABC a. Tính tỉ số các đường cao BB’ và CC’ xuất phát từ các đỉnh B và C b. Tại sao nếu AB < AC thì BB’ < CC’ ?
-
Câu 53 trang 166 Sách bài tập (SBT) Toán 8 tập 1
Hãy tính tổng các khoảng cách từ các đỉnh của hình vuông đến đường thẳng l theo a và b (a và b có cùng đơn vị đo)
