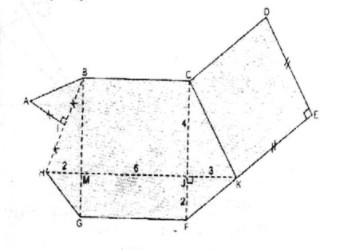
Câu 6.3 trang 165 Sách bài tập (SBT) Toán 8 tập 1Bạn Giang đã vẽ một đa giác ABCDEFGHI như ở hình bs. 26. Bạn Giang đã vẽ một đa giác ABCDEFGHI như ở hình bs. 26. Tính diện tích của đa giác đó, biết rằng : KH song song với BC (K thuộc EF); BC song song với GF; CF song song với BG; BG vuông góc với GF; CK song song với DE; CD song song với FE; KE = DE và KE vuông góc với DE; I là trung điểm của BH, AI = IH và AI vuông góc với IH; HK = 11cm, CF = 6cm. HK cắt CF tại J và JK = 3 (cm), JF = 2cm. BG cắt HK tại M và HM = 2cm. Giải:
Chia đa giác đó thành hình vuông CDEK, hình thang KFGH, hình thang BCKH và tam giác vuông AIB Ta có: MJ = KH – KJ – MH = 11 – 2 – 3 = 6(cm) ⇒ BC = GF = MJ = 6 (cm) CJ = CF – FG = 6 – 2 = 4 (cm) \(\eqalign{ & {S_{KFGH}} = {{HK + GF} \over 2}.FJ = {{11 + 6} \over 2}.2 = 17(c{m^2}) \cr & {S_{BCKH}} = {{BC + KH} \over 2}.CJ = {{11 + 6} \over 2}.4 = 34(c{m^2}) \cr} \) Trong tam giác vuông CJK có \(\widehat J = 90^\circ \). Theo định lý Pi-ta-go ta có: \(C{K^2} = C{J^2} + J{K^2} = 16 + 9 = 25 \Rightarrow CK = 5\) (cm) \({S_{CDEK}} = C{K^2} = {5^2} = 25\) (cm2 ) Trong tam giác vuông BMH có \(\widehat M = 90^\circ \).Theo định lý Pi-ta-go ta có: \(B{H^2} = B{M^2} + H{M^2}\) mà BM = CJ = 4(cm) (đường cao hình thang BCKH) \(\eqalign{ & \Rightarrow B{H^2} = {4^2} + {2^2} = 20 \cr & IB = {{BH} \over 2} \Rightarrow I{B^2} = {{B{H^2}} \over 4} = {{20} \over 4} = 5 \cr & IB = \sqrt 5 (cm) \cr} \) ∆ AIB vuông cân tại I (vì AI = IH = IB) \({S_{AIB}} = {1 \over 2}AI.IB = {1 \over 2}I{B^2} = {5 \over 2}\) ( cm2 ) \(S = {S_{CDEK}} + {S_{KFGH}} + {S_{BCKH}} + {S_{AIB}} = 25 + 17 + 34 + {5 \over 2} = {{157} \over 2}\) (cm2 )
Xem lời giải SGK - Toán 8 - Xem ngay >> Học trực tuyến lớp 8 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
Xem thêm tại đây:
Bài 6. Diện tích đa giác
|
-
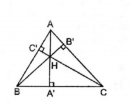
Câu 51 trang 166 Sách bài tập (SBT) Toán 8 tập 1
Cho tam giác ABC với ba đường cao AA’, BB’, CC’. Gọi H là trực tâm của tam giác đó.
-
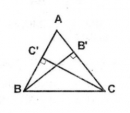
Câu 52 trang 166 Sách bài tập (SBT) Toán 8 tập 1
Cho tam giác ABC a. Tính tỉ số các đường cao BB’ và CC’ xuất phát từ các đỉnh B và C b. Tại sao nếu AB < AC thì BB’ < CC’ ?
-
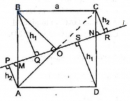
Câu 53 trang 166 Sách bài tập (SBT) Toán 8 tập 1
Hãy tính tổng các khoảng cách từ các đỉnh của hình vuông đến đường thẳng l theo a và b (a và b có cùng đơn vị đo)
-
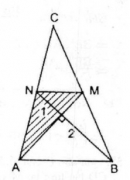
Câu 54 trang 166 Sách bài tập (SBT) Toán 8 tập 1
Tam giác ABC có hai trung tuyến AM và BN vuông góc với nhau. Hãy tính diện tích tam giác đó theo AM và BN

 Tải ngay
Tải ngay