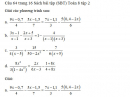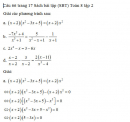Câu 63 trang 16 Sách bài tập (SBT) Toán 8 tập 2Tính gần đúng nghiệm của các phương trình sau, làm tròn đến chữ số thập phân thứ hai (dùng máy tính bỏ túi để tính toán) Tính gần đúng nghiệm của các phương trình sau, làm tròn đến chữ số thập phân thứ hai (dùng máy tính bỏ túi để tính toán) a. \(\left( {x\sqrt {13} + \sqrt 5 } \right)\left( {\sqrt 7 - x\sqrt 3 } \right) = 0\) b. \(\left( {x\sqrt {2,7} - 1,54} \right)\left( {\sqrt {1,02} + x\sqrt {3,1} } \right) = 0\) Giải: a. \(\left( {x\sqrt {13} + \sqrt 5 } \right)\left( {\sqrt 7 - x\sqrt 3 } \right) = 0\) \( \Leftrightarrow x\sqrt {13} + \sqrt 5 = 0\) hoặc \(\sqrt 7 - x\sqrt 3 = 0\) + \(x\sqrt {13} + \sqrt 5 = 0 \Leftrightarrow x = - {{\sqrt 5 } \over {\sqrt {13} }} \approx - 0,62\) + \(\sqrt 7 - x\sqrt 3 = 0 \Leftrightarrow x = {{\sqrt 7 } \over {\sqrt 3 }} \approx 1,53\) Vậy phương trình có nghiệm x = -0,62 hoặc x = 1,53. b. \(\left( {x\sqrt {2,7} - 1,54} \right)\left( {\sqrt {1,02} + x\sqrt {3,1} } \right) = 0\) \( \Leftrightarrow x\sqrt {2,7} - 1,54 = 0\) hoặc \(\sqrt {1,02} + x\sqrt {3,1} = 0\) + \(x\sqrt {2,7} - 1,54 = 0 \Leftrightarrow x = {{1,54} \over {\sqrt {2,7} }} \approx 0,94\) + \(\sqrt {1,02} + x\sqrt {3,1} = 0 \Leftrightarrow x = - {{\sqrt {1,02} } \over {\sqrt {3,1} }} \approx - 0,57\) Vậy phương trình có nghiệm x = 0,94 hoặc x = -0,57 Sachbaitap.com
Xem lời giải SGK - Toán 8 - Xem ngay >> Học trực tuyến lớp 8 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
Xem thêm tại đây:
Ôn tập chương III - Phương trình bậc nhất một ẩn
|

 Tải ngay
Tải ngay