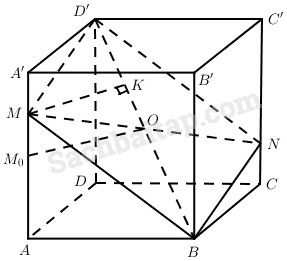
Câu 70 trang 127 Sách bài tập Hình học 11 Nâng caoGiải bài tập Câu 70 trang 127 Sách bài tập Hình học 11 Nâng cao Cắt hình lập phương bằng một mặt phẳng (P) đi qua một đường chéo của hình lập phương. Phải chọn (P) như thế nào để thiết diện thu được có diện tích nhỏ nhất. Trả lời
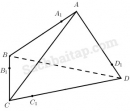
Xét (P) là mặt phẳng chứa một đường chéo, chẳng hạn đường chéo BD’ của hình lập phương. Nếu (P) chứa D’A’ thì thiết diện có diện tích là \({a^2}\sqrt 2 .\) Tương tự, nếu (P) chứa D’C’ hoặc D’D thì thiết diện cũng có diện tích là \({a^2}\sqrt 2 \). Ta xét (P) cắt AA’ tại điểm M. Gọi O là tâm hình lập phương thì MO cắt CC’ tạo N. Do đó thiết diện của hình lập phương khi cắt bởi (P) là BMD’N, đó là hình bình hành. Ta có \({S_{BM{\rm{D}}'N}} = B{\rm{D}}'.MK = d.MK\) (d là độ dài đường chéo của hình lập phương). Vậy \({S_{BM{\rm{D}}'N}}\) nhỏ nhất khi và chỉ khi MK nhỏ nhất, tức MK là đường vuông góc chung của BD’ và AA’. Dễ thấy OM0 là đường vuông góc chung của BD’ và AA’, trong đó M0 là trung điểm của AA’; \(O{M_0} = {{a\sqrt 2 } \over 2}\). Vậy lúc đó: \({S_{BMD'N}} = a\sqrt 3 .{{a\sqrt 2 } \over 2} = {{{a^2}\sqrt 6 } \over 2}\) Chú ý. Khi (P) cắt A’B' hoặc B’C’ thì cách giải quyết câu toán cũng như trên và ta có diện tích thiết diện nhỏ nhất trong trường hợp đó cũng là \({{{a^2}\sqrt 6 } \over 2}\). Dễ thấy \({{{a^2}\sqrt 6 } \over 2} < {a^2}\sqrt 2 .\) Vậy nếu (P) qua đường chéo BD’ và qua trung điểm một cạnh của hình lập phương không đi qua B và D’, thì diện tích thiết diện nhỏ nhất và có giá trị bằng \({{{a^2}\sqrt 6 } \over 2}\). Sachbaitap.com
Xem lời giải SGK - Toán 11 Nâng cao - Xem ngay >> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
Xem thêm tại đây:
Bài 5: Khoảng cách
|
-
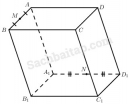
Câu 71 trang 128 Sách bài tập Hình học 11 Nâng cao
Giải bài tập Câu 71 trang 128 Sách bài tập Hình học 11 Nâng cao
-
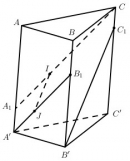
Câu 72 trang 128 Sách bài tập Hình học 11 Nâng cao
Giải bài tập Câu 72 trang 128 Sách bài tập Hình học 11 Nâng cao
-
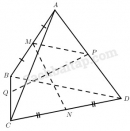
Câu 73 trang 128 Sách bài tập Hình học 11 Nâng cao
Giải bài tập Câu 73 trang 128 Sách bài tập Hình học 11 Nâng cao
-
Câu 74 trang 128 Sách bài tập Hình học 11 Nâng cao
Giải bài tập Câu 74 trang 128 Sách bài tập Hình học 11 Nâng cao

 Tải ngay
Tải ngay