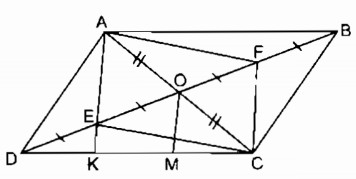
Câu 7.2 trang 91 Sách bài tập (SBT) Toán 8 tập 1Cho hình bình hành ABCD , các đường chéo cắt nhau tại O. Gọi E, F theo thứ tự là trung điểm của OD, OB. Gọi K là giao điểm của AE và CD. Chứng minh rằng: Cho hình bình hành ABCD , các đường chéo cắt nhau tại O. Gọi E, F theo thứ tự là trung điểm của OD, OB. Gọi K là giao điểm của AE và CD. Chứng minh rằng: a. AE song song CF b. DK \( = {1 \over 2}\)KC Giải:
a. Ta có: OB = OD (tính chất hình bình hành) OE \( = {1 \over 2}\)OD (gt) OF \( = {1 \over 2}\)OB (gt) Suy ra: OE = OF Xét tứ giác AECF, ta có: OE = OF (chứng minh trên) OA = OC (vì ABCD là hình bình hành) Suy ra: Tứ giác AECF là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường ) ⇒ AE // CF b. Kẻ OM // AK Trong ∆ CAK ta có: OA = OC ( chứng minh trên) OM // AK ( theo cách vẽ) ⇒ CM = MK (tính chất đường trung bình của tam giác) (1) Trong ∆ DMO ta có: DE = EO (gt) EK // OM ⇒ DK = KM (tính chất đường trung bình của tam giác) (2) Từ (1) và (2) suy ra: DK = KM = MC ⇒ DK \( = {1 \over 2}\)KC Sachbaitap.com
Xem lời giải SGK - Toán 8 - Xem ngay >> Học trực tuyến lớp 8 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
Xem thêm tại đây:
Bài 7. Hình bình hành
|
-
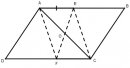
Câu 7.3 trang 91 Sách bài tập (SBT) Toán 8 tập 1
Cho hình bình hành ABCD. Lấy điểm E trên cạnh AB, điểm F trên cạnh CD sao cho AE = CF. Chứng minh rằng ba đường thẳng AC, BD, EF đồng quy.
-
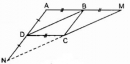
Câu 92 trang 91 Sách bài tập (SBT) Toán 8 tập 1
Cho hình 13 trong đó ABCD là hình bình hành. Chứng minh rằng điểm M đối xứng với điểm N qua điểm C.
-
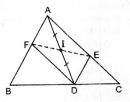
Câu 93 trang 92 Sách bài tập (SBT) Toán 8 tập 1
Cho hình 14 trong đó DE // AB, DF // AC. Chứng minh rằng điểm E đối xưng với điểm F qua điểm I.
-
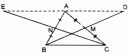
Câu 94 trang 92 Sách bài tập (SBT) Toán 8 tập 1
Cho tam giác ABC, các đường trung tuyến BM, CN. Gọi D là điểm đối xứng với B qua M, gọi E là điểm đối xứng với C qua N. Chứng minh rằng điểm D đối xứng với điểm E qua điểm A.

 Tải ngay
Tải ngay