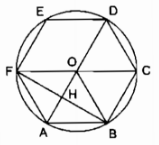
Câu 74 trang 114 Sách Bài Tập (SBT) Toán 9 Tập 2Chứng minh rằng đường chéo BF chia AD thành hai đoạn thẳng theo tỉ số 1: 3. Cho lục giác ABCDEF. Chứng minh rằng đường chéo BF chia AD thành hai đoạn thẳng theo tỉ số 1: 3. Giải
Lục giác đều ABCDEF nội tiếp trong đường tròn (O) \(\overparen{AB}\) = \(\overparen{CB}\) = \(\overparen{CD}\) = \(\overparen{DE}\) = \(\overparen{EF}\) = \(\overparen{FA}\) = 600 \( \Rightarrow \) sđ \(\overparen{ABCD}\) = sđ \(\overparen{AB}\) + sđ \(\overparen{BC}\) + sđ \(\overparen{CD}\) = 1800 Nên AD là đường kính của đường tròn (O) Ta có: OA = OB = OF = AB = AF = R Nên tứ giác ABOF là hình thoi Gọi giao điểm của AD và BF là H Ta có: \(FB \bot OA\) (tính chất hình thoi) \( \Rightarrow AH = HO = {{AO} \over 2} = {R \over 2}\) \(HD = HO + OD = {R \over 2} + R = {{3R} \over 2}\) Suy ra: \({{AH} \over {HD}} = {{{R \over 2}} \over {{{3R} \over 2}}} = {1 \over 3}\) Sachbaitap.com
Xem lời giải SGK - Toán 9 - Xem ngay >> Học trực tuyến lớp 9 và Lộ trình UP10 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Lộ trình học tập 3 giai đoạn: Học nền tảng lớp 9, Ôn thi vào lớp 10, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
Xem thêm tại đây:
Bài tập ôn chương III - Góc với đường tròn
|
-
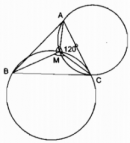
Câu 75 trang 114 Sách Bài Tập (SBT) Toán 9 Tập 2
Dựng điểm M nằm trong tam giác ABC sao cho góc AMB = góc BMC = góc CMA.
-
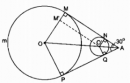
Câu 76 trang 114 Sách Bài Tập (SBT) Toán 9 Tập 2
Tìm độ dài của dây cua- roa mắc qua hai ròng rọc.
-
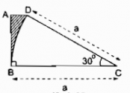
Câu 77 trang 114 Sách Bài Tập (SBT) Toán 9 Tập 2
Tính diện tích phần gạch sọc trên hình sau (theo kích thước đã cho trên hình)
-
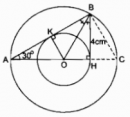
Câu 78 trang 114 Sách Bài Tập (SBT) Toán 9 Tập 2
a) Chứng minh đường tròn (O; OH) tiếp xúc với cạnh AB.

 Tải ngay
Tải ngay