Giải SGK Toán 11 Kết nối tri thức tập 2 trang 75Giải bài 8.6, 8.7, 8.8, 8.9, 8.10 trang 75 SGK Toán lớp 11 Kết Nối Tri Thức tập 2. Một hộp đựng 8 viên bi màu xanh và 6 viên bi màu đỏ, có cùng kích thước và khối lượng. Bạn Sơn lấy ngẫu nhiên một viên bi từ hộp (lấy xong không trả lại vào hộp). Tiếp đó đến lượt bạn Tùng lấy ngẫu nhiên một viên bi từ hộp đó. Tính xác suất để bạn Tùng lấy được viên bi màu xanh. Bài 8.6 trang 75 SGK Toán 11 - Kết Nối Tri Thức tập 2 Một hộp đựng 8 viên bi màu xanh và 6 viên bi màu đỏ, có cùng kích thước và khối lượng. Bạn Sơn lấy ngẫu nhiên một viên bi từ hộp (lấy xong không trả lại vào hộp). Tiếp đó đến lượt bạn Tùng lấy ngẫu nhiên một viên bi từ hộp đó. Tính xác suất để bạn Tùng lấy được viên bi màu xanh. Phương pháp: Nếu A và B là hai biến cố xung khắc thì \(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right)\) Lời giải: Gọi A là biến cố “Bạn Sơn lấy được viên bi màu xanh, bạn Tùng lấy được viên bi màu xanh”; B là biến cố “Bạn Sơn lấy được viên bi màu đỏ, bạn Tùng lấy được viên bi màu xanh”. Do đó, biến cố “bạn Tùng lấy được viên bi màu xanh” là biến cố hợp của A và B. Vì A và B là hai biến cố xung khắc nên ta áp dụng công thức cộng xác suất cho hai biến cố xung khắc có: P(A∪ B) = P(A) + P(B). + Không gian mẫu Ω: Hộp bao gồm: 6 + 8 = 14 viên bi Mỗi phần tử của Ω được chọn bởi hai công đoạn: Công đoạn 1: Bạn Sơn lấy ngẫu nhiên một viên bi từ hộp (lấy xong không trả lại vào hộp). Có Công đoạn 2: Sau công đoạn 1, hộp còn lại 13 viên bi. Bạn Tùng lấy lấy ngẫu nhiên một viên bi từ hộp đó. Có Theo quy tắc nhân, ta có: n(Ω) = 14 . 13 = 182. + Tính P(A): Mỗi phần tử của A được chọn bởi hai công đoạn: Công đoạn 1: Bạn Sơn lấy ngẫu nhiên một viên bi trong 8 viên bi màu xanh từ hộp (lấy xong không trả lại vào hộp). Có 8 cách chọn. Công đoạn 2: Bạn Tùng lấy ngẫu nhiên một viên bi trong 7 viên bi màu xanh còn lại trong hộp đó. Có 7 cách chọn. Theo quy tắc nhân, ta có: n(A) = 8 . 7 = 56. Suy ra: P(A) = + Tính P(B): Mỗi phần tử của B được chọn bởi hai công đoạn: Công đoạn 1: Bạn Sơn lấy ngẫu nhiên một viên bi trong 6 viên bi màu đỏ từ hộp (lấy xong không trả lại vào hộp). Có 6 cách chọn. Công đoạn 2: Bạn Tùng lấy ngẫu nhiên một viên bi trong 8 viên bi màu xanh còn lại trong hộp đó. Có 8 cách chọn. Theo quy tắc nhân, ta có: n(B) = 6 . 8 = 48. Suy ra: P(B) = Do đó, ta có: P(A∪ B) = P(A) + P(B) = Vậy xác suất để bạn Tùng lấy được viên bi màu xanh là Bài 8.7 trang 75 SGK Toán 11 - Kết Nối Tri Thức tập 2
Lớp 11A của một trường có 40 học sinh, trong đó có 14 bạn thích nhạc cổ điển, 13 bạn thích nhạc trẻ và 5 bạn thích cả nhạc cổ điển và nhạc trẻ. Chọn ngẫu nhiên một bạn trong lớp. Tính xác suất để: a) Bạn đó thích nhạc cổ điển hoặc nhạc trẻ; b) Bạn đó không thích cả nhạc cổ điển và nhạc trẻ. Phương pháp:Công thức cộng xác suất \(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {AB} \right)\) Công thức xác suất của biến cố đối \(P\left( A \right) = 1 - P\left( {\overline A } \right)\) Lời giải: Gọi A là biến cố “Bạn đó thích nhạc cổ điển”; B là biến cố “Bạn đó thích nhạc trẻ”; C là biến cố “Bạn đó thích nhạc cổ điển hoặc nhạc trẻ”. Biến cố “Bạn đó thích cả nhạc cổ điển và nhạc trẻ” là biến cố giao của A và B. Do đó, ta có: C = A∪ B. Biến cố a) Áp dụng công thức cộng xác suất ta có: P(C) = P(A∪ B) = P(A) + P(B) – P(AB) Ta cần tính: P(A), P(B), P(AB). + Không gian mẫu Ω là tập hợp các học sinh của lớp 11A nên n(Ω) = 40. + Tính P(A): Biến cố A là tập hợp các học sinh thích nhạc cổ điển nên n(A) = 14. Suy ra: P(A) = + Tính P(B): Biến cố B là tập hợp các học sinh thích nhạc trẻ nên n(B) = 13. Suy ra: P(B) = + Tính P(AB): Biến cố giao của A và B là tập hợp các học sinh thích cả nhạc cổ điển và nhạc trẻ nên n(AB) = 5. Suy ra: P(AB) = Do đó, P(C) = P(A) + P(B) – P(AB) = Vậy xác suất để bạn được chọn thích nhạc cổ điển hoặc nhạc trẻ là b) Áp dụng công thức tính xác suất của biến cố đối ta có: P( Vậy xác suất để bạn được chọn không thích cả nhạc cổ điển và nhạc trẻ là Bài 8.8 trang 75 SGK Toán 11 - Kết Nối Tri Thức tập 2 Một khu phố có 50 hộ gia đình nuôi chó hoặc nuôi mèo, trong đó có 18 hộ nuôi chó, 16 hộ nuôi mèo và 7 hộ nuôi cả chó và mèo. Chọn ngẫu nhiên một hộ trong khu phố trên. Tính xác suất để: a) Hộ đó nuôi chó hoặc nuôi mèo; b) Hộ đó không nuôi cả chó và mèo. Phương pháp: Công thức cộng xác suất \(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {AB} \right)\) Công thức xác suất của biến cố đối \(P\left( A \right) = 1 - P\left( {\overline A } \right)\) Lời giải: Gọi A là biến cố “Hộ đó nuôi chó” ; B là biến cố “Hộ đó nuôi mèo” ; C là biến cố “Hộ đó nuôi cả chó và mèo” ; D là biến cố “Hộ đó nuôi chó hoặc nuôi mèo”. Như vậy, ta có: C = A ∩ B; D = A∪ B.
a) Áp dụng công thức cộng xác suất ta có: P(D) = P(A∪ B) = P(A) + P(B) – P(AB) = P(A) + P(B) – P(C) Ta cần tính P(A), P(B), P(C) + Không gian mẫu Ω là tập hợp 50 hộ gia đình nên n(Ω) = 50. + Tính P(A): Biến cố A là tập hợp các hộ gia đình nuôi chó nên n(A) = 18. Suy ra: P(A) = + Tính P(B): Biến cố B là tập hợp các hộ gia đình nuôi mèo nên n(B) = 16. Suy ra: P(B) = + Tính P(C): Biến cố C là tập hợp các hộ gia đình nuôi cả chó và mèo nên n(C) = 7. Suy ra: P(C) = Do đó, ta có: P(D) = P(A) + P(B) – P(C) = Vậy xác suất để hộ được chọn nuôi chó hoặc mèo là b) Áp dụng công thức tính xác suất cho biến cố đối ta có: P( ) = 1 – P(D) = 1 – Vậy xác suất để hộ được chọn không nuôi cả chó và mèo là Bài 8.9 trang 75 SGK Toán 11 - Kết Nối Tri Thức tập 2 Một nhà xuất bản phát hành hai cuốn sách A và B. Thống kê cho thấy có 50% người mua sách A; 70% người mua sách B; 30% người mua cả sách A và sách B. Chọn ngẫu nhiên một người mua. Tính xác suất để: a) Người mua đó mua ít nhất một trong hai sách A hoặc B, b) Người mua đó không mua cả sách A và sách B. Phương pháp: Công thức cộng xác suất \(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {AB} \right)\) Công thức xác suất của biến cố đối \(P\left( A \right) = 1 - P\left( {\overline A } \right)\) Lời giải: a) Gọi E là biến cố “Người đó mua cuốn sách A”; F là biến cố “Người đó mua cuốn sách B” ; G là biến cố “Người đó mua cả hai cuốn sách A và B”; H là biến cố “Người đó mua ít nhất một trong hai sách A và B”. Như vậy ta có: G = E ∩ F ; H = E∪ F. Áp dụng công thức cộng xác suất ta có: P(H) = P(E∪ F) = P(E) + P(F) – P(EF) = P(E) + P(F) – P(G) Lại có: P(E) = 50% = 0,5 P(F) = 70% = 0,7 P(G) = 30% = 0,3 Do đó, ta có: P(H) = P(E) + P(F) – P(G) = 0,5 + 0,7 – 0,3 = 0,9. Vậy xác suất để người đó mua ít nhất một trong hai sách A và B là 0,9. b) Gọi Áp dụng công thức xác suất cho biến cố đối ta có: P( Vậy xác suất để người đó không mua cả sách A và sách B là 0,1. Bài 8.10 trang 75 SGK Toán 11 - Kết Nối Tri Thức tập 2 Một nhà xuất bản phát hành hai cuốn sách A và B. Thống kê cho thấy có 50% người mua sách A; 70% người mua sách B; 30% người mua cả sách A và sách B. Chọn ngẫu nhiên một người mua. Tính xác suất để: a) Người mua đó mua ít nhất một trong hai sách A hoặc B, b) Người mua đó không mua cả sách A và sách B. Phương pháp: Công thức cộng xác suất \(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {AB} \right)\) Công thức xác suất của biến cố đối \(P\left( A \right) = 1 - P\left( {\overline A } \right)\) Lời giải: Gọi A là biến cố “Giáo viên môn Toán tham khảo bộ sách A”; B là biến cố “Giáo viên môn Toán tham khảo bộ sách B”. Do đó, A ∩ B là biến cố “Giáo viên Toán tham khảo cả hai bộ sách A và B”; C = A ∪ B là biến cố “Giáo viên Toán tham khảo ít nhất một trong hai bộ sách A và B”. Biến cố đối của C là biến cố Ta có: P(A) = 63% = 0,63 P(B) = 56% = 0,56 P(AB) = 28,5% = 0,285 Áp dụng công thức cộng xác suất ta có: P(C) = P(A ∪ B) = P(A) + P(B) – P(AB) = 0,63 + 0,56 – 0,285 = 0,905. Áp dụng công thức xác suất cho biến cố đối ta có: P( Vậy xác suất để giáo viên đó không tham khảo cả hai bộ sách giáo khoa A và B là 0,095. Tức là, tỉ lệ có 9,5%giáo viên môn Toán tại các trường trung học phổ thông của tỉnh đó không tham khảo cả hai bộ sách giáo khoa A và B. Sachbaitap.com
Xem thêm tại đây:
Bài 29. Công thức cộng xác suất
|
-

Giải SGK Toán 11 Kết nối tri thức tập 2 trang 78
Giải bài 8.11, 8.12, 8.13, 8.14, 8.15 trang 78 SGK Toán lớp 11 Kết Nối Tri Thức tập 2. Cho hai biến cố A và B là hai biến cố xung khắc với P(A) > 0, P(B) > 0. Chứng tỏ rằng hai biến cố A và B không độc lập.

 Tải ngay
Tải ngay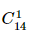 = 14 (cách chọn).
= 14 (cách chọn).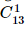 = 13 (cách chọn)
= 13 (cách chọn)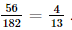 .
.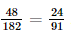
 .
.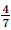
 là biến cố “Bạn đó không thích cả nhạc cổ điển và nhạc trẻ”.
là biến cố “Bạn đó không thích cả nhạc cổ điển và nhạc trẻ”.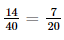
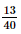 .
.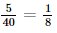
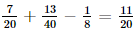
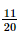
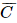 ) = 1 – P(C) = 1 –
) = 1 – P(C) = 1 – 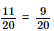 .
.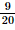
 là biến cố đối của D, tức là
là biến cố đối của D, tức là  là biến cố “Hộ đó không nuôi cả chó và mèo”.
là biến cố “Hộ đó không nuôi cả chó và mèo”.
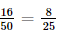 .
.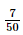
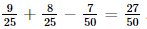 .
.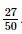 .
.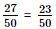 .
.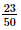
 là biến cố đối của H, tức là
là biến cố đối của H, tức là  là biến cố “Người đó không mua cả sách A và sách B”.
là biến cố “Người đó không mua cả sách A và sách B”.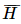 ) = 1 – P(H) = 1 – 0,9 = 0,1.
) = 1 – P(H) = 1 – 0,9 = 0,1.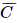 : “Giáo viên Toán không tham khảo cả hai bộ sách giáo khoa A và B”.
: “Giáo viên Toán không tham khảo cả hai bộ sách giáo khoa A và B”.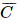 ) = 1 – P(C) = 1 – 0,905 = 0,095.
) = 1 – P(C) = 1 – 0,905 = 0,095.