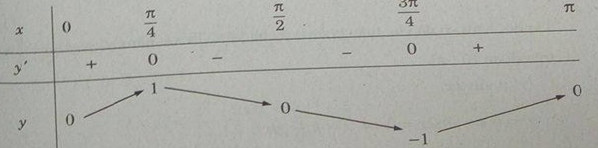
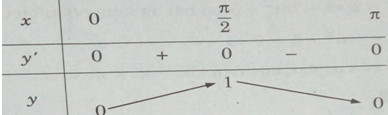
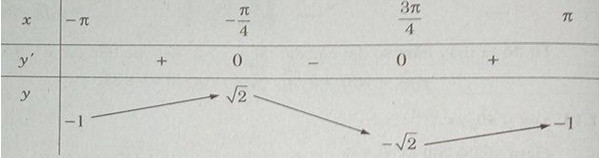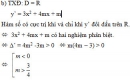Bài 1.14 trang 15 Sách bài tập (SBT) Giải tích 12Tìm cực trị của các hàm số sau: Tìm cực trị của các hàm số sau: a) \(y = \sin 2x\) b) \(y = \cos x - \sin x\) c) \(y = {\sin ^2}x\) Hướng dẫn làm bài: a) \(y = \sin 2x\) Hàm số có chu kỳ \(T = \pi \) Xét hàm số \(y = \sin 2x\) trên đoạn \({\rm{[}}0;\pi {\rm{]}}\) , ta có: \(y' = 2\cos 2x\) \(y = 0 \Leftrightarrow \left[ \matrix{ Bảng biến thiên: Do đó trên đoạn \({\rm{[}}0;\pi {\rm{]}}\) , hàm số đạt cực đại tại \({\pi \over 4}\) , đạt cực tiểu tại \({{3\pi } \over 4}\) và \({y_{CD}} = y({\pi \over 4}) = 1;\,\,{y_{CT}} = y({{3\pi } \over 4}) = - 1\) Vậy trên R ta có: \({y_{CĐ}} = y({\pi \over 4} + k\pi ) = 1;\) \({y_{CT}} = y({{3\pi } \over 4} + k\pi ) = - 1,k \in Z\) b) Hàm số tuần hoàn chu kỳ nên ta xét trên đoạn \({\rm{[}} - \pi ;\pi {\rm{]}}\). \(\eqalign{ Lập bảng biến thiên trên đoạn \({\rm{[}} - \pi ;\pi {\rm{]}}\) Hàm số đạt cực đại tại \(x = - {\pi \over 4} + k2\pi \) , đạt cực tiểu tại \(x = {{3\pi } \over 4} + k2\pi (k \in Z)\) và \({y_{CĐ}} = y( - {\pi \over 4} + k2\pi ) = \sqrt 2\) ; \({y_{CT}} = y({{3\pi } \over 4} + k2\pi ) = - \sqrt 2 (k \in Z)\) c) Ta có: \(y = {\sin ^2}x = {{1 - \cos 2x} \over 2}\) Do đó, hàm số đã cho tuần hoàn với chu kỳ \(\pi \). Ta xét hàm số \(y = {1 \over 2} - {1 \over 2}\cos 2x\) trên đoạn \({\rm{[}}0;\pi {\rm{]}}\) . \(\eqalign{ Lập bảng biến thiên trên đoạn \(\left[ {0,\pi } \right]\) Từ đó, ta thấy hàm số đạt cực tiểu tại \(x = k.{\pi \over 2}\) với k chẵn, đạt cực đại tại \(x = k.{\pi \over 2}\) với k lẻ, và \({y_{CT}} = y(2m\pi ) = 0;\) \({y_{CĐ}} = y((2m + 1){\pi \over 2}) = 1(m \in Z)\) Sachbaitap.com
Xem lời giải SGK - Toán 12 - Xem ngay >> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
Xem thêm tại đây:
Bài 2. Cực trị của hàm số - SBT Toán 12
|
-

Bài 1.16 trang 15 Sách bài tập (SBT) Giải tích 12
Xác định giá trị của tham số m để hàm số y = x3 – 2x2 + mx + 1 đạt cực tiểu tại x = 1.
-
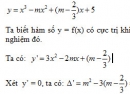
Bài 1.17 trang 16 Sách bài tập (SBT) Giải tích 12
Khi đó, hàm số đạt cực tiểu hay đạt cực đại? Tính cực trị tương ứng.
-
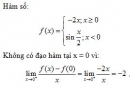
Bài 1.18 trang 16 Sách bài tập (SBT) Giải tích 12
Chứng minh rằng hàm số sau không có đạo hàm tại x = 0 nhưng đạt cực đại tại điểm đó.

 Tải ngay
Tải ngay