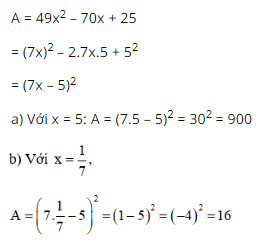Bài 20, 21, 22, 23, 24, 25 trang 12 SGK Toán 8 tập 1 - Luyện tậpGiải bài 20, 21, 22, 23, 24, 25 trang 12 SGK Toán 8 tập 1 bài Luyện tập. Bài 21. Viết các đa thức sau dưới dạng bình phương của một tổng hoặc một hiệu: Bài 20 trang 12 SGK Toán lớp 8 tập 1 Câu hỏi: Nhận xét sự đúng, sai của kết quả sau: \({x^2} + 2xy + 4{y^2} = {\left( {x + 2y} \right)^2}\) Phương pháp: Áp dụng bình phương của một tổng. \({\left( {A + B} \right)^2} = {A^2} + 2AB + {B^2}\) Lời giải: Kết quả trên sai. Ta có: (x + 2y)2 = x2 + 2.x.2y + 4y2 = x2 + 4xy + 4y2 ≠ x2 + 2xy + 4y2. Bài 21 trang 12 SGK Toán lớp 8 tập 1 Câu hỏi: Viết các đa thức sau dưới dạng bình phương của một tổng hoặc một hiệu: a) \(9{x^2}-6x + 1\); b) \({\left( {2x{\rm{ }} + {\rm{ }}3y} \right)^2} + 2.\left( {2x + 3y} \right) + 1\). Hãy nêu một đề bài tương tự. Phương pháp: Áp dụng bình phương của một tổng, bình phương của một hiệu. \({\left( {A + B} \right)^2} = {A^2} + 2AB + {B^2}\) \({\left( {A - B} \right)^2} = {A^2} - 2AB + {B^2}\) Lời giải: a) 9x2 – 6x + 1 = (3x)2 – 2.3x.1 + 12 = (3x – 1)2 (Áp dụng hằng đẳng thức (2) với A = 3x; B = 1) b) (2x + 3y)2 + 2.(2x + 3y) + 1 = (2x + 3y)2 + 2.(2x + 3y).1 + 12 = [(2x + 3y) +1]2 (Áp dụng hằng đẳng thức (1) với A = 2x + 3y ; B = 1) = (2x + 3y + 1)2 c) Đề bài tương tự: Viết các đa thức sau dưới dạng bình phương của một tổng hoặc hiệu : 4x2 – 12x + 9 (2a + b)2 – 4.(2a + b) + 4. Bài 22 trang 12 SGK Toán lớp 8 tập 1 Câu hỏi: Tính nhanh: a. \({101^2};\) b. \({199^2};\) c. \(47.53\) Phương pháp: a. Áp dụng: \({\left( {A + B} \right)^2} = {A^2} + 2AB + {B^2}\) b. Áp dụng: \({\left( {A - B} \right)^2} = {A^2} - 2AB + {B^2}\) c. Áp dụng: \({A^2} - {B^2} = \left( {A + B} \right)\left( {A - B} \right)\) Lời giải: a) 1012 = (100 + 1)2 = 1002 + 2.100 + 1 = 10000 + 200 + 1 = 10201 b) 1992 = (200 – 1)2 = 2002 – 2.200 + 1 = 40000 – 400 + 1 = 39601 c) 47.53 = (50 – 3)(50 + 3) = 502 – 32 = 2500 – 9 = 2491. Bài 23 trang 12 SGK Toán lớp 8 tập 1 Câu hỏi: Chứng minh rằng: \({\left( {a + b} \right)^2} = {\left( {a - b} \right)^2} + 4ab;\) \({\left( {a - b} \right)^2} = {\left( {a + b} \right)^2} - 4ab.\) Áp dụng: a) Tính \({\left( {a - b} \right)^2}\), biết \(a + b = 7\) và \(a . b = 12.\) b) Tính \({\left( {a + b} \right)^2}\), biết \(a - b = 20\) và \(a . b = 3.\) Phương pháp: Áp dụng bình phương của một tổng, bình phương của một hiệu để biến đổi vế trái hoặc vế phải của từng đẳng thức, đưa về bằng vế còn lại. \({\left( {A + B} \right)^2} = {A^2} + 2AB + {B^2}\) \({\left( {A - B} \right)^2} = {A^2} - 2AB + {B^2}\) Lời giải: + Chứng minh (a + b)2 = (a – b)2 + 4ab Ta có: VP = (a – b)2 + 4ab = a2 – 2ab + b2 + 4ab = a2 + (4ab – 2ab) + b2 = a2 + 2ab + b2 = (a + b)2 = VT (đpcm) + Chứng minh (a – b)2 = (a + b)2 – 4ab Ta có: VP = (a + b)2 – 4ab = a2 + 2ab + b2 – 4ab = a2 + (2ab – 4ab) + b2 = a2 – 2ab + b2 = (a – b)2 = VT (đpcm) + Áp dụng, tính: a) (a – b)2 = (a + b)2 – 4ab = 72 – 4.12 = 49 – 48 = 1 b) (a + b)2 = (a – b)2 + 4ab = 202 + 4.3 = 400 + 12 = 412 Bài 24 trang 12 SGK Toán lớp 8 tập 1 Câu hỏi: Tính giá trị của biểu thức \(49{x^2}-70x + 25\) trong mỗi trường hợp sau: a) \(x = 5\); b) \(x = \dfrac{1}{7}\). Phương pháp: Áp dụng bình phương của một hiệu, sau đó thay lần lượt từng giá trị của \(x\) để tính giá trị của biểu thức. Lời giải:
Bài 25 trang 12 SGK Toán lớp 8 tập 1 Câu hỏi: Tính: a. \({\left( {a + b + c} \right)^2}\); b. \({\left( {a + b - c} \right)^2}\); c. \({\left( {a - b - c} \right)^2}\) Phương pháp: Áp dụng bình phương của một tổng, bình phương của một hiệu. \({\left( {A + B} \right)^2} = {A^2} + 2AB + {B^2}\) \({\left( {A - B} \right)^2} = {A^2} - 2AB + {B^2}\) Lời giải: a) (a + b + c)2 = [(a + b) + c]2 = (a + b)2 + 2(a + b)c + c2 = a2 + 2ab + b2 + 2ac + 2bc + c2 = a2 + b2 + c2 + 2ab + 2bc + 2ac b) (a + b – c)2 = [(a + b) – c]2 = (a + b)2 – 2(a + b)c + c2 = a2 + 2ab + b2 – 2ac – 2bc + c2 = a2 + b2 + c2 + 2ab – 2bc – 2ac c) (a – b – c)2 = [(a – b) – c]2 = (a – b)2 – 2(a – b)c + c2 = a2 – 2ab + b2 – 2ac + 2bc + c2 = a2 + b2 + c2 – 2ab + 2bc – 2ac. Sachbaitap.com
Xem thêm tại đây:
Chương I. Phép nhân và phép chia các đa thức
|
-

Bài 26, 27, 28, 29 trang 14 SGK Toán 8 tập 1 - Những hằng đẳng thức đáng nhớ (tiếp)
Giải bài 26, 27, 28, 29 trang 14 SGK Toán 8 tập 1, bài những hằng đẳng thức đáng nhớ (tiếp). Bài 29 Đố: Đức tính đáng quý. Hãy viết mỗi biểu thức sau dưới dạng bình phương hoặc lập phương của một tổng hoặc một hiệu.
-

Bài 30, 31, 32, 33, 34, 35, 36, 37, 38 trang 16, 17 SGK Toán 8 tập 1 - Những hằng đẳng thức đáng nhớ (tiếp) - Luyện tập
Giải bài 30, 31, 32, 33, 34, 35, 36, 37, 38 trang 16, 17 SGK Toán 8 tập 1, bài Những hằng đẳng thức đáng nhớ (tiếp) - Luyện tập. Bài 37. Dùng bút chì nối các biểu thức sao cho chúng tạo thành hai vế của một hằng đẳng thức (theo mẫu)
-

Bài 39, 40, 41, 42 trang 19 SGK Toán 8 tập 1 - Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung
Giải bài 39, 40, 41, 42 trang 19 SGK Toán 8 tập 1 - Bài Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung. Bài 42. Chứng minh rằng 55^n+1 - 55^n chia hết cho 54 (với n là số tự nhiên).
-

Bài 43, 44, 45, 46 trang 20, 21 SGK Toán 8 tập 1 - Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức
Giải bài 43, 44, 45 trang 20, bài 46 trang 21 SGK Toán 8 tập 1 - Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức. Bài 46: Tính nhanh: a) 732 - 272 ; b) 372 - 132 ; c) 20022 - 22

 Tải ngay
Tải ngay