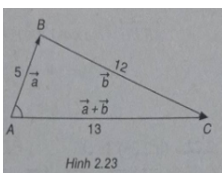
Bài 2.19 trang 92 Sách bài tập (SBT) Toán Hình học

Cho hai véc tơ \(\overrightarrow a \) và \(\overrightarrow b \) có \(\left| {\overrightarrow a } \right| = 5,\left| {\overrightarrow b } \right| = 12\) và \(\left| {\overrightarrow a  + \overrightarrow b } \right| = 13\). Tính tích vô hướng \(\overrightarrow a .(\overrightarrow a  + \overrightarrow b )\) và suy ra góc giữa hai vec tơ \(\overrightarrow a \) và \(\overrightarrow a  + \overrightarrow b \)

Gợi ý làm bài

(h.2.23)

Dựng tam giác ABC có AB = 5, BC= 12 và AC = 13.

Ta có \(\left| {\overrightarrow a } \right| = 5,\left| {\overrightarrow b } \right| = 12\) và \(\left| {\overrightarrow a  + \overrightarrow b } \right| = 13\)

Và \(\overrightarrow {AB}  = \overrightarrow a ,\overrightarrow {BC}  = \overrightarrow b ,\overrightarrow {AC}  = \overrightarrow a  + \overrightarrow b \)

Khi đó \(\overrightarrow a (\overrightarrow a  + \overrightarrow b ) = \overrightarrow {AB} .\overrightarrow {AC} \)

Mặt khác ta có:

\(\overrightarrow {AB} .\overrightarrow {AC}  = {1 \over 2}(A{C^2} + A{B^2} - B{C^2})\)

\( = {1 \over 2}({13^2} + {5^2} - {12^2}) = 25\)

Ta suy ra:

\(\eqalign{
& \cos (\overrightarrow {AB} .\overrightarrow {AC} ) = {{\overrightarrow {AB} .\overrightarrow {AC} } \over {\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|}} \cr
& = {{25} \over {5.13}} \approx 0,3846 \cr} \)

Suy ra \((\overrightarrow {AB} .\overrightarrow {AC} ) \approx {67^0}23'\)

Sachbaitap.net