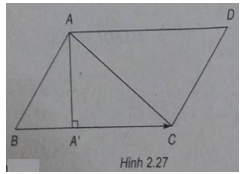
Bài 2.23 trang 92 Sách bài tập (SBT) Toán Hình học 10

Trong mặt phẳng Oxy cho tam giác ABC với A = (2;4), B = ( - 3;1) và C = (3;1). Tính:

a) Tọa độ điểm D để tứ giác ABCD là hình bình hành;

b) Tọa độ chân của đường cao vẽ từ đỉnh A.

Gợi ý làm bài

(h.2.27)

a) Vì ABCD là hình bình hành nên ta có:

\(\overrightarrow {BD}  = \overrightarrow {BA}  + \overrightarrow {BC} \) trong đó \(\overrightarrow {BA}  = (5;3)\)

\(\overrightarrow {BC}  = (6; - 2)\)

\( =  > \,\overrightarrow {BD}  = (11;1)\)

Giả sử D có tọa độ \(({x_D},{y_D})\)

Vì \(\overrightarrow {BD}  = (11;1)\) và B(-3; 1) nên ta có:

\(\left\{ \matrix{
{x_D} + 3 = 11 \hfill \cr
{y_D} - 1 = 1 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
{x_D} = 8 \hfill \cr
{y_D} = 2 \hfill \cr} \right.\)

Chú ý: Ta có thể dựa vào biểu thức vec tơ \(\overrightarrow {AD}  = \overrightarrow {BC} \) hoặc \(\overrightarrow {CD}  = \overrightarrow {BA} \) để tính tọa độ điểm D.

b) Gọi A(x;y) là chân đường cao vẽ từ A ta có:

\(\left\{ \matrix{
\overrightarrow {AA'} \bot \overrightarrow {BC} \,hay\overrightarrow {AA'} .\overrightarrow {BC} = 0 \hfill \cr
\overrightarrow {BA'} cung\,phuong\,voi\,\overrightarrow {BC} \hfill \cr} \right.\)

Với 

\(\eqalign{
& \overrightarrow {AA'} = (x - 2;y - 4), \cr
& \overrightarrow {BC} = (6; - 2), \cr
& \overrightarrow {BA'} = (x + 3;y - 1) \cr} \)

Do đó:

\(\left\{ \matrix{
(x - 2).6 + (y - 4).( - 2) = 0 \Leftrightarrow \overrightarrow {AA'} \bot \overrightarrow {BC} \hfill \cr
- 2(x + 3) = 6(y - 1) = 0 \Leftrightarrow \overrightarrow {BA'\,} cung\,phuong\,voi\,\overrightarrow {BC} \hfill \cr} \right.\)

\(\left\{ \matrix{
(x - 2).6 + (y - 4).( - 2) = 0 \Leftrightarrow \overrightarrow {AA'} \bot \overrightarrow {BC} \hfill \cr
- 2(x + 3) = 6(y - 1) = 0 \Leftrightarrow \overrightarrow {BA'} cung\,phuong\,voi\,\overrightarrow {BC} \hfill \cr} \right.\)

\(\eqalign{
& \Leftrightarrow \left\{ \matrix{
6x - 12 - 2y + 8 = 0 \hfill \cr
- 2x - 6 - 6y + 6 = 0 \hfill \cr} \right. \cr
& \Leftrightarrow \left\{ \matrix{
6x - 2y - 4 = 0 \hfill \cr
- 2x - 6y = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
{x_{A'}} = {3 \over 5} \hfill \cr
{y_{A'}} = - {1 \over 5} \hfill \cr} \right. \cr} $\)

Sachbaitap.net