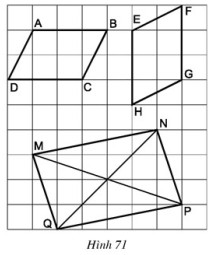
Bài 43, 44, 45 trang 92 SGK Toán 8 tập 1 - Hình bình hành

Bài 43 trang 92 SGK Toán lớp 8 tập 1

Câu hỏi:

Các tứ giác \(ABCD, EFGH, MNPQ\) trên giấy kẻ ô vuông ở hình \(71\) có là hình bình hành hay không ?

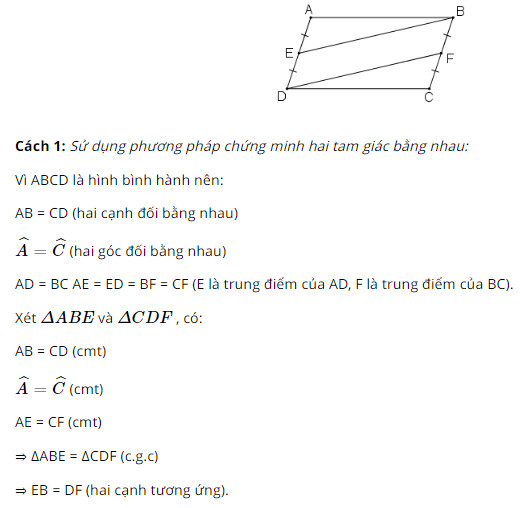
Phương pháp:

Áp dụng dấu hiệu nhận biết hình bình hành:

+) Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.

+)  Tứ giác có các cạnh đối bằng nhau là hình bình hành

Lời giải:

Cả ba tứ giác là hình bình hành

- Tứ giác ABCD là hình bình hành vì có AB // CD và AB = CD = 3 (dấu hiệu nhận biết 3)

- Tứ giác EFGH là hình bình hành vì có EH // FG và EH = FG = 3 (dấu hiệu nhận biết 3)

- Tứ giác MNPQ là hình bình hành vì có MN = PQ và MQ = NP (dấu hiệu nhận biết 2)

- Với các tứ giác ABCD, EFGH còn có thể nhận biết là hình bình hành bằng dấu hiệu nhận biết 2.

- Với tứ giác MNPQ còn có thể nhận biết là hình bình hành bằng dấu hiệu nhận biết 5.)

Bài 44 trang 92 SGK Toán lớp 8 tập 1

Câu hỏi:

Cho hình bình hành \(ABCD\). Gọi  \(E\) là trung điểm của \(AD\), \(F\) là trung điểm của \(BC\). Chứng minh rằng \(BE = DF\).

Phương pháp:

Áp dụng:

+) Hình bình hành có các cặp cạnh đối song song và bằng nhau.

+) Dấu hiệu nhận biết hình bình hành: Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.

Lời giải:

Bài 45 trang 92 SGK Toán lớp 8 tập 1

Câu hỏi:

Cho hình bình hành \(ABCD\) (\(AB > BC\)). Tia phân giác của góc \(D\) cắt \(AB\) ở \(E\), tia phân giác của góc \(B\) cắt \(CD\) ở \(F\).

a) Chứng minh rằng \(DE // BF\).

b) Tứ giác \(DEBF\) là hình gì ? Vì sao ?

Phương pháp:

Áp dụng:

+) Hình bình hành có các góc đối bằng nhau. 

+) Dấu hiệu nhận biết hình bình hành: Tứ giác có các cạnh đối song song là hình bình hành.

Lời giải:

Sachbaitap.com