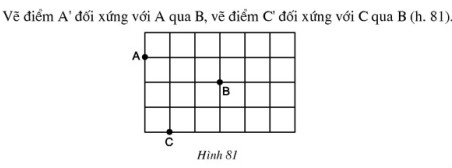
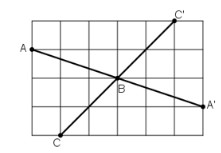
Bài 50, 51, 52, 53 trang 95, 96 SGK Toán 8 tập 1 - Đối xứng tâmBài 50 trang 95,bài 51, 52, 53 trang 96 SGK Toán 8 tập 1 - Đối xứng tâm. Bài 53 Cho hình (82), trong đó (MD // AB) và (ME // AC). Chứng minh rằng điểm (A) đối xứng với điểm (M) qua điểm (I). Bài 50 trang 95 SGK Toán lớp 8 tập 1 Câu hỏi:
Phương pháp: Áp dụng định nghĩa: Hai điểm gọi là đối xứng với nhau qua điểm \(O\) nếu \(O\) là trung điểm của đoạn thẳng nối hai điểm đó. Lời giải:
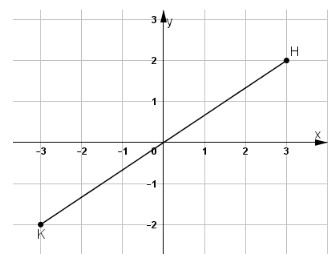
Bài 51 trang 96 SGK Toán lớp 8 tập 1 Câu hỏi: Trong mặt phẳng tọa độ, cho điểm \(H\) có tọa độ \((3; 2)\). Hãy vẽ điểm \(K\) đối xứng với \(H\) qua gốc tọa độ và tìm tọa độ \(K\). Phương pháp: Định nghĩa: Hai điểm \(A\) và \(A'\) gọi là đối xứng với nhau qua điểm \(O\) nếu \(O\) là trung điểm của \(AA'.\) Lời giải: K đối xứng với H qua gốc tọa độ ⇔ O(0; 0) là trung điểm của KH. Dựa vào hình biểu diễn ta có K(-3; -2).
Bài 52 trang 96 SGK Toán lớp 8 tập 1 Câu hỏi: Cho hình bình hành \(ABCD\). Gọi \(E\) là điểm đối xứng với \(D\) qua điểm \(A\), gọi \(F\) là điểm đối xứng với \(D\) qua điểm \(C\). Chứng minh rằng điểm \(E\) đối xứng với điểm \(F\) qua điểm \(B\). Phương pháp: Áp dụng: +) Hình bình hành có các cặp cạnh đối song song và bằng nhau. +) Hai điểm gọi là đối xứng với nhau qua điểm \(O\) nếu \(O\) là trung điểm của đoạn thẳng nối hai điểm đó. +) Tiên đề ơclit: Qua một điểm ở ngoài đường thẳng chỉ có một đường thẳng song song với đường thẳng đó. Lời giải: Ta có: ABCD là hình bình hành nên: AD//BC, AD = BC Mà AE = AD (E đối xứng với D qua A) ⇒ BC = AE. Xét tứ giác AEBC có BC // AE, BC = AE nên AEBC là hình bình hành ⇒ EB // AC và EB = AC (1). Xét tam giác DEF, có: A là trung điểm DE ( D và E đối xứng qua A) C là trung điểm của DF ( D và F đối xứng qua C) ⇒">⇒⇒ AC là đường trung bình của tam giác DEF ⇒ AC // EF, AC = 12">1212 EF (2) Từ (1) và (2) suy ra E, B, F thẳng hàng (theo tiên đề Ơ – clit) và BE = BF ⇒ B là trung điểm EF ⇒ E đối xứng với F qua B
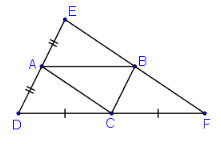
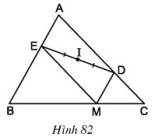
Bài 53 trang 96 SGK Toán lớp 8 tập 1 Câu hỏi: Cho hình \(82\), trong đó \(MD // AB\) và \(ME // AC\). Chứng minh rằng điểm \(A\) đối xứng với điểm \(M\) qua điểm \(I\).
Phương pháp: Áp dụng: +) Dấu hiệu nhận biết hình bình hành: Tứ giác có các cạnh đối song song. +) Hình bình hành có hai đường chéo cắt nhau tại trung điểm mỗi đường. +) Hai điểm gọi là đối xứng với nhau qua điểm \(O\) nếu \(O\) là trung điểm của đoạn thẳng nối hai điểm đó. Lời giải: Ta có: MD// AE (vì MD// AB) ME // AD (vì ME // AC) Nên AEMD là hình bình hành, I là trung điểm của DE nên I cũng là trung điểm của AM, do đó A đối xứng với M qua I. Sachbaitap.com
Xem thêm tại đây:
Chương I. Tứ giác
|
-

Bài 54, 55, 56, 57 trang 96 SGK Toán 8 tập 1 - Luyện tập
Bài 54, 55, 56, 57 trang 96 SGK Toán 8 tập 1 - Luyện tập. Bài 55 Cho hình bình hành (ABCD), (O) là giao điểm của hai đường chéo. Một đường thẳng đi qua (O) cắt các cạnh (AB) và (CD) theo thứ tự ở (M) và (N). Chứng minh rằng điểm (M) đối xứng với điểm (N) qua (O).
-

Bài 58, 59, 69, 61 trang 99 SGK Toán 8 tập 1 - Hình chữ nhật
Bài 58, 59, 69, 61 trang 99 SGK Toán 8 tập 1 - Hình chữ nhật. Bài 61 Cho tam giác (ABC), đường cao (AH). Gọi (I) là trung điểm của (AC, E) là điểm đối xứng với (H) qua (I). Tứ giác (AHCE) là hình gì ? Vì sao ?
-
Bài 62, 63, 64, 65, 66 trang 99, 100 SGK Toán 8 tập 1 - Luyện tập
Bài 62 trang 99,bài 63, 64, 65, 66 trang 100 SGK Toán 8 tập 1 - Luyện tập. Bài 65 Tứ giác (ABCD) có hai đường chéo vuông góc với nhau. Gọi (E, F, G, H) theo thứ tự là trung điểm của các cạnh (AB, BC, CD, DA). Tứ giác (EFGH) là hình gì? Vì sao?
-
Bài 67, 68, 69 trang 102, 103 SGK Toán 8 tập 1 - Đường thẳng song song với một đường thẳng cho trước
Bài 67, 68 trang 102, bài 69 trang 103 SGK Toán 8 tập 1 - Đường thẳng song song với một đường thẳng cho trước. Bài 68 Cho điểm (A) nằm ngoài đường thẳng (d) và có khoảng cách đến (d) bằng (2cm). Lấy điểm (B) bất kì thuộc đường thẳng (d). Gọi (C) là điểm đối xứng với điểm (A) qua điểm (B).

 Tải ngay
Tải ngay