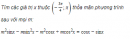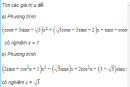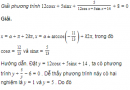Câu 1.31 trang 12 sách bài tập Đại số và Giải tích 11 Nâng caoChứng minh a) Từ khẳng định (khi x thay đổi, hàm số \(y = \sin x\) nhận mọi giá trị tùy ý thuộc đoạn \(\left[ { - 1;1} \right]\)”, hãy chứng minh rằng: khi x thay đổi, hàm số \(y = a\sin x + b\cos x\) (a, b là hằng số, \({a^2} + {b^2} \ne 0\)) lấy mọi giá trị tùy ý thuộc đoạn \(\left[ { - \sqrt {{a^2} + {b^2}} ;\sqrt {{a^2} + {b^2}} } \right]\) b) Xét hàm số \(y = {{\sin x + \cos x - 1} \over {\sin x - \cos x + 3}}\). Viết đẳng thức đó thành \(\left( {y - 1} \right)\sin x - \left( {y + 1} \right)\cos x = - 3y - 1,\) để suy ra rằng khi x thay đổi, hàm số trên lấy mọi giá trị y tùy ý thỏa mãn điều kiện. \({\left( {y - 1} \right)^2} + {\left( {y + 1} \right)^2} \ge {\left( {3y + 1} \right)^2}\) Từ đó hãy tìm giá trị lớn nhất và nhỏ nhất của hàm số đã cho. c) Tìm giá trị lớn nhất và nhỏ nhất của hàm số \(y = {{\cos x + 2\sin x + 3} \over {2\cos x - \sin x + 4}}\) Giải a) Ta có \(a\sin x + b\cos x = \sqrt {{a^2} + {b^2}} \sin \left( {x + \alpha } \right)\) nên dễ thấy hàm số y nhận mọi giá trị tùy ý thuộc đoạn \(\left[ { - \sqrt {{a^2} + {b^2}} ;\sqrt {{a^2} + {b^2}} } \right]\) b) Do \(\left| {\sin x + \cos x} \right| \le \sqrt 2 \) nên \(\sin x - \cos x + 3 \ne 0\) với mọi x. Vậy cặp số \(\left( {x,y} \right)\) thỏa mãn \(y = {{\sin x + \cos x - 1} \over {\sin x - \cos x + 3}}\) khi và chỉ khi: \(\left( {y - 1} \right)\sin x - \left( {y + 1} \right)\cos x = - \left( {3y + 1} \right)\) Với mọi giá trị y cho trước, biểu thức ở vế trái của đẳng thức này lấy mọi giá trị tùy ý thuộc đoạn \(\left[ { - \sqrt {{{\left( {y - 1} \right)}^2} + {{\left( {y + 1} \right)}^2}} ;\sqrt {{{\left( {y - 1} \right)}^2} + {{\left( {y + 1} \right)}^2}} } \right].\) Đẳng thức trên cho thấy \( - \left( {3y + 1} \right)\) phải thuộc đoạn đó, tức là: \({\left( {3y + 1} \right)^2} \le {\left( {y - 1} \right)^2} + {\left( {y + 1} \right)^2}\) Vậy với mọi y thỏa mãn điều kiện này, tồn tại x để \(\left( {y - 1} \right)\sin x - \left( {y + 1} \right)\cos x = - \left( {3y + 1} \right)\) Để ý rằng bất đẳng thức trên tương đương với \(7{y^2} + 6y - 1 \le 0\) tức là \( - 1 \le y \le {1 \over 7}\) Từ đó suy ra giá trị lớn nhất và giá trị nhỏ nhất của y theo thứ tự là \({1 \over 7}\) và -1. c) \(y = {{\cos x + 2\sin x + 3} \over {2\cos x - \sin x + 4}}\) Để ý rằng \(\left| {2\cos x - \sin x} \right| \le \sqrt 5 ,\) nên \(2\cos x - \sin x + 4 \ne 0\) với mọi x. Vậy \(\left( {x,y} \right)\) thỏa mãn đẳng thức trên khi và chỉ khi \(\left( {y + 2} \right)\sin x + \left( {1 - 2y} \right)\cos x = 4y - 3\) Lập luận tương tự như câu b), hàm số y lấy mọi giá trị sao cho \({\left( {4y - 3} \right)^2} \le {\left( {y + 2} \right)^2} + {\left( {1 - 2y} \right)^2}\) Bất đẳng thức tương đương với \(11{y^2} - 24y + 4 \le 0\) tức là \({2 \over {11}} \le y \le 2\) Vậy giá trị lớn nhất và giá trị nhỏ nhất của y theo thứ tự là 2 và \({2 \over {11}}\) sachbaitap.com
Xem lời giải SGK - Toán 11 Nâng cao - Xem ngay >> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
Xem thêm tại đây:
Bài 3. Một số dạng phương trình lượng giác đơn giản
|

 Tải ngay
Tải ngay