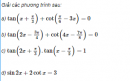Câu 1.38 trang 14 sách bài tập Đại số và Giải tích 11 Nâng caoSố đo của một trong các góc của tam giác vuông ABC là nghiệm của phương trình Số đo của một trong các góc của tam giác vuông ABC là nghiệm của phương trình \({\sin ^3}x + \sin x\sin 2 x - 3{\cos ^3}x = 0\) Chứng minh ABC là tam giác vuông cân. Giải Giả sử một góc của tam giác vuông ABC có số đo độ thỏa mãn phương trình đã cho . Ta viết phương trình đã cho thành \({\sin ^3}x + 2{\sin ^2}x\cos x - 3{\cos ^3}x = 0\) (1) \(({0^o} < x \le {90^o})\) Dễ thấy \(x = {90^o}\) không phải nghiệm của phương trình , vậy \(\cos x \ne 0\) và ta có thể chia 2 vế phương trình cho \({\cos ^3}x\) được : (1)\( \Leftrightarrow {\tan ^3}x + 2\tan x - 3 = 0 \) \(\Leftrightarrow \left( {\tan x - 1} \right)\left( {{{\tan }^2}x + 3\tan x + 3} \right) = 0\) Vì phương trình \({\tan ^2}x + 3\tan x + 3 = 0\) vô ngiệm , nên (1)\( \Leftrightarrow \tan x = 1\) . Kết hợp với điều kiện \({0^o} < x < {90^o}\) ta thấy chỉ có \(x = {45^o}\) là thỏa mãn. Từ đó suy ra tam giác ABC là tam giác vuông cân. sachbaitap.com
Xem lời giải SGK - Toán 11 Nâng cao - Xem ngay >> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
Xem thêm tại đây:
Bài 3. Một số dạng phương trình lượng giác đơn giản
|
-
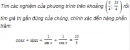
Câu 1.45 trang 15 sách bài tập Đại số và Giải tích 11 Nâng cao
Tìm các nghiệm của phương trình trên khoảng
-

Câu 1.46 trang 15 sách bài tập Đại số và Giải tích 11 Nâng cao
Biết rằng các số rađian của ba góc của tam giác ABC là nghiệm của phương trình

 Tải ngay
Tải ngay