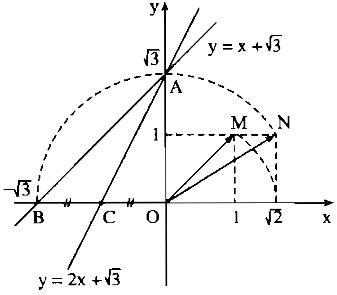
Câu 14 trang 64 Sách Bài Tập (SBT) Toán 9 Tập 1a) Vẽ đồ thị của các hàm số sau trên cũng một mặt phẳng tọa độ: a) Vẽ đồ thị của các hàm số sau trên cũng một mặt phẳng tọa độ: \(y = x + \sqrt 3\); (1) \(y = 2x + \sqrt 3 \); (2) b) Gọi giao điểm của đường thẳng \(y = x + \sqrt 3 \) với các trục Oy, Ox theo thứ tự là A, B và giao điểm của đường thẳng \(y = 2x + \sqrt 3 \) với các trục Oy, Ox theo thứ tự là A, C. Tính các góc của tam giác ABC (dùng máy tính bỏ túi CASIO fx-220 hoặc CASIO fx-500A). Gợi ý làm bài: a) *Vẽ đồ thị của hàm số \(y = x + \sqrt 3 \) Cho x = 0 thì \(y = \sqrt 3 \). Ta có: \(A\left( {0;\sqrt 3 } \right)\) Cho y = 0 thì \(x + \sqrt 3 = 0 \Rightarrow x = - \sqrt 3 \). Ta có: \(B\left( { - \sqrt 3 ;0} \right)\) Cách tìm điểm có tung độ bằng \(\sqrt 3 \) trên trục Oy: - Dựng điểm M(1;1). Ta có: \(OM = \sqrt 2 \) - Dựng cung tròn tâm O bán kính OM cắt trục Ox tại điểm có hoành độ bằng \(\sqrt 2 \) . - Dựng điểm \(N\left( {1;\sqrt 2 } \right)\). Ta có: \(ON = \sqrt 3 \) - Vẽ cung tròn tâm O bán kính ON cắt trục Oy tại A có tung độ \(\sqrt 3 \) cắt tia đối của Ox tại B có hoành độ \(-\sqrt 3 \) . Đồ thị của hàm số \(y = x + \sqrt 3 \) là đường thẳng AB. *Vẽ đồ thị của hàm số \(y = 2x + \sqrt 3 \) Cho x = 0 thì \(y = \sqrt 3 \). Ta có: \(A\left( {0;\sqrt 3 } \right)\) Cho y = 0 thì \(2x + \sqrt 3 = 0 \Rightarrow x = - {{\sqrt 3 } \over 2}\). Ta có: \(C\left( { - {{\sqrt 3 } \over 2};0} \right)\) Đồ thị của hàm số \(y = 2x + \sqrt 3 \) là đường thẳng AC
b) Ta có: \(tg\widehat {ABO} = {{OA} \over {OB}} = {{\sqrt 3 } \over {\sqrt 3 }} = 1 \Rightarrow \widehat {ABO} = {45^0}\) hay \(\widehat {ABC} = {45^0}\) \(tg\widehat {ACO} = {{OA} \over {OC}} = {{\sqrt 3 } \over {{{\sqrt 3 } \over 2}}} = 2 \Rightarrow \widehat {ACO} = {63^0}26'\) Ta có: \(\widehat {ACO} + \widehat {ACB} = {180^0}\) (hai góc kề bù) Suy ra : \(\widehat {ACB} = {180^0} - \widehat {ACO} = {180^0} - {63^0}26' = {116^0}34'\) Lại có: \(\widehat {ACB} + \widehat {ABC} + \widehat {BAC} = {180^0}\) Suy ra: \(\eqalign{ Sachbaitap.com
Xem lời giải SGK - Toán 9 - Xem ngay >> Học trực tuyến lớp 9 và Lộ trình UP10 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Lộ trình học tập 3 giai đoạn: Học nền tảng lớp 9, Ôn thi vào lớp 10, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
Xem thêm tại đây:
Bài 3. Đồ thị của hàm số y=ax+b (a≠0)
|
-
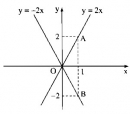
Câu 15 trang 64 Sách Bài Tập (SBT) Toán 9 Tập 1
a) Với các giá trị nào của m thì hàm số đồng biến ? Nghịch biến ?
-
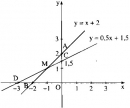
Câu 16 trang 64 Sách Bài Tập (SBT) Toán 9 Tập 1
a) Xác định giá trị của a để đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 2.
-
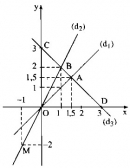
Câu 17 trang 64 Sách Bài Tập (SBT) Toán 9 Tập 1
a) Vẽ trên cùng hệ trục tọa độ Oxy đồ thị các hàm số sau:
-
Câu 18 trang 65 Sách Bài Tập (SBT) Toán 9 Tập 1
Hãy xác đinh hệ số a trong mỗi trường hợp sau:

 Tải ngay
Tải ngay