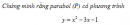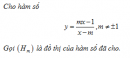Câu 1.63 trang 23 sách bài tập Giải tích 12 Nâng caoChứng minh rằng các đồ thị của ba hàm số Chứng minh rằng các đồ thị của ba hàm số \(f(x) = {x^2} - 3x + 4,g(x) = 1 + {1 \over x}\) và \(h(x) = - 4x + 6\sqrt x \) Tiếp xúc với nhau tại một điểm. Giải Phương trình hoành độ giao điểm của f(x) và g(x) là: \(\eqalign{ Vậy f(x) và g(x) giao nhau tại A (1; 2) Ta có: \(-4.1+6.\sqrt 1=2\) Do đó A thuộc đồ thị của hàm số h(x) Mặt khác: \(f'\left( 1 \right) = g'\left( 1 \right) = h'\left( 1 \right) = - 1\) Do đó ba hàm số đã cho tiếp xúc với nhau tại A (1; 2) Sachbaitap.com
Xem lời giải SGK - Toán 12 Nâng cao - Xem ngay >> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
Xem thêm tại đây:
Bài 8. Một số bài toán thường gặp về đồ thị
|
-

Câu 1.65 trang 23 sách bài tập Giải tích 12 Nâng cao
Chứng minh rằng có hai tiếp tuyến chung của parabol
-
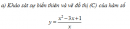
Câu 1.67 trang 23 sách bài tập Giải tích 12 Nâng cao
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số

 Tải ngay
Tải ngay