Tải ngay
Câu 29 trang 160 Sách bài tập (SBT) Toán 8 tập 1Hai cạnh của một tam giác có độ dài là 5cm và 6cm. Hỏi diện tích của tam giác đó có thể lấy giá trị nào trong các giá trị sau: Hai cạnh của một tam giác có độ dài là 5cm và 6cm. Hỏi diện tích của tam giác đó có thể lấy giá trị nào trong các giá trị sau: a. 10 \(c{m^2}\) b. 15 \(c{m^2}\) c. 20 \(c{m^2}\) Giải: Giả sử hai cạnh của tam giác là 5cm và 6cm. Chiều cao tương ứng của hai tam giác là h và k. \({S_1} = {1 \over 2}.5.h;{S_2} = {1 \over 2}.6.k\) h và k là đường cao ứng với cạnh đáy là 5 và 6. Theo tính chất của đường vuông góc và đường xiên thì h ≤ 5 và k ≤ 6 Suy ra diện tích của tam giác S ≤ 18 Vậy diện tích của tam giác có thể bằng 10 \(c{m^2}\) hay 15 \(c{m^2}\) nhưng không thể bằng 20 \(c{m^2}\)
Xem lời giải SGK - Toán 8 - Xem ngay >> Học trực tuyến lớp 8 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều). Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả.
Xem thêm tại đây:
Bài 3. Diện tích tam giác
|
-
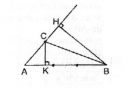
Câu 30 trang 160 Sách bài tập (SBT) Toán 8 tập 1
Cho tam giác ABC, biết AB = 3AC. Tính tỉ số hai đường cao xuất phát từ các đỉnh B và C.
-
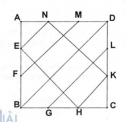
Câu 31 trang 160 Sách bài tập (SBT) Toán 8 tập 1
Tính diện tích của ngũ giác AEPSN và của tứ giác PQRS, biết AB = 6cm.
-
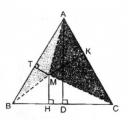
Câu 3.2 trang 161 Sách bài tập (SBT) Toán 8 tập 1
Cho tam giác đều ABC và điểm M bất kì nằm trong tam giác đó. Đường thẳng đi qua điểm M và vuông góc với BC tại điểm H. Đường thẳng đi qua điểm M và vuông góc với CA tại điểm K. Đường thẳng đi qua điểm M và vuông góc với AB tại điểm T.
-
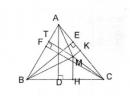
Câu 3.3 trang 161 Sách bài tập (SBT) Toán 8 tập 1
Cho hai tam giác ABC và DBC. Kẻ đường cao AH của tam giác ABC. Kẻ đường cao DK của tam giác DBC. Gọi S là diện tích của tam giác ABC. Gọi S’ là diện tích của tam giác DBC.
