Câu 30 trang 10 Sách bài tập (SBT) Toán 8 tập 2Giải các phương trình bậc hai sau đây bằng cách đưa về dạng phương trình tích. Giải các phương trình bậc hai sau đây bằng cách đưa về dạng phương trình tích. a. \({x^2} - 3x + 2 = 0\) b. \(- {x^2} + 5x - 6 = 0\) c. \(4{x^2} - 12x + 5 = 0\) d. \(2{x^2} + 5x + 3 = 0\) Giải: a. \({x^2} - 3x + 2 = 0\) \( \Leftrightarrow {x^2} - x - 2x + 2 = 0\) \(\eqalign{ & \Leftrightarrow x\left( {x - 1} \right) - 2\left( {x - 1} \right) = 0 \cr & \Leftrightarrow \left( {x - 2} \right)\left( {x - 1} \right) = 0 \cr} \) \( \Leftrightarrow x - 2 = 0\) hoặc \(x - 1 = 0\) + \(x - 2 = 0 \Leftrightarrow x = 2 \) + \(x - 1 = 0 \Leftrightarrow x = 1\) Vậy phương trình có nghiệm x = 2 hoặc x = 1. b. \( - {x^2} + 5x - 6 = 0\) \( \Leftrightarrow - {x^2} + 2x + 3x - 6 = 0\) \(\eqalign{ & \Leftrightarrow - x\left( {x - 2} \right) + 3\left( {x - 2} \right) = 0 \cr & \Leftrightarrow \left( {x - 2} \right)\left( {3 - x} \right) = 0 \cr} \) \( \Leftrightarrow x - 2 = 0\) hoặc \(3 - x = 0\) + \(x - 2 = 0 \Leftrightarrow x = 2\) + \(3 - x = 0 \Leftrightarrow x = 3\) Vậy phương trình có nghiệm x = 2 hoặc x = 3 c. \(4{x^2} - 12x + 5 = 0\) \(\eqalign{ & \Leftrightarrow 4{x^2} - 2x - 10x + 5 = 0 \cr & \Leftrightarrow 2x\left( {2x - 1} \right) - 5\left( {2x - 1} \right) = 0 \cr & \Leftrightarrow \left( {2x - 1} \right)\left( {2x - 5} \right) = 0 \cr} \) \( \Leftrightarrow 2x - 1 = 0\) hoặc \(2x - 5 = 0\) + \(2x - 1 = 0 \Leftrightarrow x = 0,5\) + \(2x - 5 = 0 \Leftrightarrow x = 2,5\) Vậy phương trình có nghiệm x = 0,5 hoặc x = 2,5 d. \(2{x^2} + 5x + 3 = 0\) \(\eqalign{ & \Leftrightarrow 2{x^2} + 2x + 3x + 3 = 0 \cr & \Leftrightarrow 2x\left( {x + 1} \right) + 3\left( {x + 1} \right) = 0 \cr & \Leftrightarrow \left( {x + 1} \right)\left( {2x + 3} \right) = 0 \cr} \) \( \Leftrightarrow 2x + 3 = 0\) hoặc \(x + 1 = 0\) + \(2x + 3 = 0 \Leftrightarrow x = - 1,5\) + \(x + 1 = 0 \Leftrightarrow x = - 1\) Vậy phương trình có nghiệm x = -1,5 hoặc x = -1 Sachbaitap.com
Xem lời giải SGK - Toán 8 - Xem ngay >> Học trực tuyến lớp 8 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
Xem thêm tại đây:
Bài 4. Phương trình tích
|
-
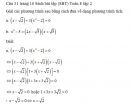
Câu 31 trang 10 Sách bài tập (SBT) Toán 8 tập 2
Giải các phương trình sau bằng cách đưa về dạng phương trình tích:
-

Câu 33 trang 11 Sách bài tập (SBT) Toán 8 tập 2
Biết rằng x = -2 là một trong các nghiệm của phương trình:

 Tải ngay
Tải ngay







