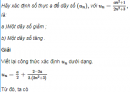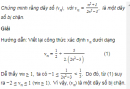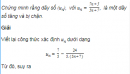Tải ngay
Câu 3.17 trang 89 sách bài tập Đại số và Giải tích 11 Nâng caoXét tính đơn điệu của các dãy số sau: Xét tính đơn điệu của các dãy số sau: a) Dãy số \(({a_n})\) với \({a_n} = {{3{n^2} - 2n + 1} \over {n + 1}};\) b) Dãy số \(({b_n})\) với \({b_n} = {{{n^2} + n + 1} \over {2{n^2} + 1}}.\) Giải a) Viết lại công thức xác định số hạng tổng quát của dãy số \(({a_n})\) dưới dạng \({a_n} = 3n - 5 + {6 \over {n + 1}}\) Từ đó, ta có với mọi \(n \ge 1:\) \({a_{n + 1}} - {a_n} = 3 + 6.\left( {{1 \over {n + 2}} - {1 \over {n + 1}}} \right) = {{3.\left( {\left( {n + 1} \right)\left( {n + 2} \right) - 2} \right)} \over {\left( {n + 1} \right)\left( {n + 2} \right)}} \) \(= {{3n\left( {n + 3} \right)} \over {\left( {n + 1} \right)\left( {n + 2} \right)}} > 0\) Vì thế, \(({a_n})\) là một dãy số tăng.
sachbaitap.com
Xem lời giải SGK - Toán 11 Nâng cao - Xem ngay >> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
Xem thêm tại đây:
Bài 2. Dãy số
|
-
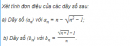
Câu 3.18 trang 89 sách bài tập Đại số và Giải tích 11 Nâng cao
Xét tính đơn điệu của các dãy số sau:
