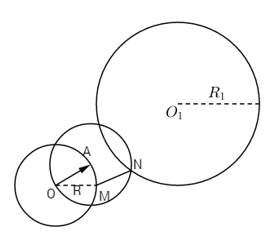
Câu 4 trang 6 Sách bài tập Hình Học 11 nâng cao.

Bình chọn:

3.7 trên 6 phiếu

Xác định điểm M trên (O; R).

4. Trang 6 Sách bài tập Hình Học 11 nâng cao.

Cho hai đường tròn không đồng tâm (O; R) và \((O_1;R_1)\) và một điểm A trên (O; R). Xác định điểm M trên (O; R) và điểm N trên \(\left( {{O_1};\,{R_1}} \right)\) sao cho \(\overrightarrow {MN} = \overrightarrow {OA} \).

Giải

Giả sử đã xác định được M và N theo yêu cầu của bài toán. Khi đó, phép tịnh tiến T theo vecto \(\overrightarrow {OA} \) sẽ biến điểm M thành điểm N và biến đường tròn (O; R) thành đường tròn (A; R). Vì (O; R) đi qua M, nên (A; R) đi qua N. Do đó N là giao điểm của hai đường tròn (A; R) và \(\left( {{O_1};\,{R_1}} \right)\). Từ đó dễ dàng suy ra cách dựng.

Số nghiệm hình phụ thuộc vào số giao điểm của hai đường tròn (A; R) và \(\left( {{O_1};\,{R_1}} \right)\).

sachbaitap.com

Báo lỗi - Góp ý

Xem lời giải SGK - Toán 11 Nâng cao - Xem ngay

>> Học trực tuyến Lớp 11 cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng. Cam kết giúp học sinh lớp 11 học tốt, hoàn trả học phí nếu học không hiệu quả.