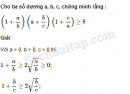Câu 4.16 trang 104 SBT Đại số 10 Nâng caoGiải bài tập Câu 4.16 trang 104 SBT Đại số 10 Nâng cao. Để chứng minh \(x\left( {1 - x} \right) \le \dfrac{1}{4}\) với mọi x, bạn An đã làm như sau : Áp dụng bất đẳng thức giữa trung bình cộng và trung bình nhân cho hai số \(x\) và \(1 – x\), ta có \(\sqrt {{\rm{x}}\left( {1 - x} \right)} \le \dfrac{{{\rm{x}} + 1 - x}}{2} = \dfrac{1}{2}\) Do đó \(x\left( {1 - x} \right) \le \dfrac{1}{4}\) Theo em, bạn An giải như thế đúng hay sai, vì sao ? Em giải bài này như thế nào ? Giải: Bạn An giải như vậy là sai. Sai lầm của bạn An là không để ý điều kiện của các số a, b trong bất đẳng thức giữa trung bình cộng và trung bình nhân \(\dfrac{{a + b}}{2} \ge \sqrt {{\rm{a}}b} \) là \(a ≥ 0, b ≥ 0\). Trong bài này \(x\) và \(1 – x\) chỉ không âm khi \(x \in \left[ {0;1} \right].\) Lời giải đúng là : \(x\left( {1 - x} \right) \le \dfrac{1}{4} \Leftrightarrow - {x^2} + {\rm{x}} \le \dfrac{1}{4}\) \(\Leftrightarrow {x^2} - x + \dfrac{1}{4} \ge 0 \Leftrightarrow {\left( {{\rm{x}} - \dfrac{1}{2}} \right)^2} \ge 0,\) bất đẳng thức này hiển nhiên đúng với mọi x. Sachbaitap.com
Xem thêm tại đây:
Bài 1. Bất đẳng thức và chứng minh bất đẳng thức
|

 Tải ngay
Tải ngay