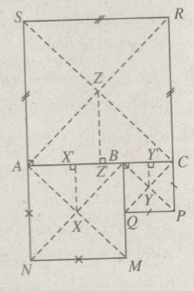
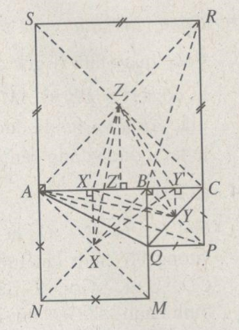
Câu 46 trang 12 Sách bài tập Hình Học 11 nâng cao.Gọi X, Y, Z lần lượt là trung điểm của các đoạn thẳng AB, BC, AC. 46. Trang 12 Sách bài tập Hình Học 11 nâng cao. Trên hình 1 có ba điểm thẳng hàng A, B, C và ba hình vuông ABMN, BCPQ, ACRS với tâm lần lượt là X, Y, Z. Gọi X, Y, Z lần lượt là trung điểm của các đoạn thẳng AB, BC, AC. a) Chứng minh rằng các tam giác Z’XY, X'YZ, Y’XZ là những tam giác vuông cân. b) Chứng minh rằng hai đoạn thẳng AY, XZ bằng nhau và vuông góc với nhau, cũng như thế đối với hai đoạn BZ, XY và CX, YZ.
Giải a) Phép quay tâm B góc quay \({90^o}\) biến A thành M và Q thành C. Bởi vậy, biến đoạn thẳng AQ thành MC. Suy ra hai đoạn thẳng AQ, MC bằng nhau và vuông góc với nhau. Chú ý rằng Z’X là đường trung bình của tam giác AMC, còn Z’Y là đường trung bình của tam giác CAQ nên tam giác Z’XY vuông cân tại đỉnh Z’. Dùng phép quay tâm C góc quay \({90^o}\) ta chứng minh được đoạn thẳng PA, BR bằng nhau và vuông góc với nhau. Suy ra X’YZ là tam giác vuông cân tại X’. Tương tự cũng chứng minh được Y’XZ là tam giác vuông cân tại Y’.
b) Phép quay tâm X’ góc quay \({90^o}\) biến điểm A thành điểm X và biến Y thành điểm Z. Suy ra hai đoạn thẳng AY, XZ bằng nhau và vuông góc với nhau. sachbaitap.com
Xem lời giải SGK - Toán 11 Nâng cao - Xem ngay >> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
Xem thêm tại đây:
Bài 4: Phép quay và phép đối xứng tâm
|
-

Câu 47 trang 12 Sách bài tập Hình Học 11 Nâng cao
Cho hai tam giác ABC và A’B’C’ với đường cao lần lượt là AH và A’H’. Trong mỗi trường hợp dưới đây, hai tam giác đó có bằng nhau hay không?
-

Câu 48 trang 12 Sách bài tập Hình Học 11 Nâng cao
Chứng minh rằng hai hình thang ấy bằng nhau nếu AB = A’B’, BC = B’C’ và CD = C’D’.
-

Câu 49 trang 12 Sách bài tập Hình Học 11 Nâng cao
Chứng minh rằng hai tam giác bằng nhau nếu có các đường tròn nội tiếp bằng nhau, một cặp đường tròn bàng tiếp bằng nhau, đồng thời khoảng cách giữa tâm đường tròn nội tiếp và bàng tiếp của hai tam giác đó cũng bằng nhau.
-
Câu 50 trang 13 Sách bài tập Hình Học 11 Nâng cao
Chứng minh rằng hai tam giác vuông bằng nhau nếu có các cạnh huyền bằng nhau và đường cao ứng với cạnh huyền bằng nhau.

 Tải ngay
Tải ngay