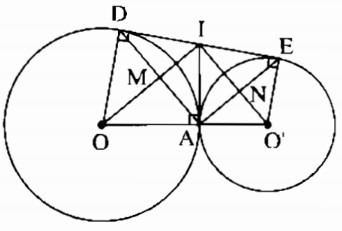
Câu 82 trang 171 Sách bài tập (SBT) Toán 9 Tập 1Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài DE, D ∈ (O), E ∈ (O’). Kẻ tiếp tuyến chung tại A, cắt DE ở I. Gọi M là giao điểm của OI và AD, N là giao điểm của O’I và AE. Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài DE, D ∈ (O), E ∈ (O’). Kẻ tiếp tuyến chung tại A, cắt DE ở I. Gọi M là giao điểm của OI và AD, N là giao điểm của O’I và AE. a) Tứ giác AMIN là hình gì ? Vì sao ? b) Chứng minh hệ thức IM.IO = IN.IO’. c) Chứng minh rằng OO’ là tiếp tuyến của đường tròn có đường kính là DE. d) Tính độ dài DE biết rằng OA = 5cm, O’A = 3,2cm. Giải:
a) Trong đường tròn (O) ta có OI là tia phân giác của góc AID ( tính chất hai tiếp tuyếnc cắt nhau) Trong đường tròn (O’) ta có O’I là tia phân giác của góc AIE ((tính chất hai tiếp tuyến cắt nhau) nên IO ⊥ IO' ( tính chất kề bù) Suy ra: \(\widehat {OIO'} = 90^\circ \) hay \(\widehat {MIN} = 90^\circ \) Lại có: IA = ID ((tính chất hai tiếp tuyến cắt nhau) Suy ra tam giác ADI có IO là phân giác của góc AID nên IO cũng là đường cao của tam giác AID. Suy ra: IO ⊥ AD hay \(\widehat {AMI} = 90^\circ \) Mặt khác: IA = IE ((tính chất hai tiếp tuyến cắt nhau) Suy ra tam giác AEI cân tại I. Tam giác cân AIE có IO' là phân giác của góc AIE nên IO¢ cũng là đường cao của tam giác AIE. Suy ra: IO' ⊥ AE hay \(\widehat {ANI} = 90^\circ \) Tứ giác AMIN có ba góc vuông nên nó là hình chữ nhật. b) Tam giác AIO vuông tại A có AM ⊥ IO. Theo hệ thức lượng trong tam giác vuông, ta có: IA2 = IM.IO (1) Tam giác AIO' vuông tại A có AN ⊥ IO'. Theo hệ thức lượng trong tam giác vuông, ta có: IA2 = IN.IO' (2) Từ (1) và (2) suy ra: IM.IO = IN.IO' c) Ta có: IA = ID = IE ( chứng minh trên) Suy ra A nằm trên đường tròn tâm I đường kính DE. Vì OO' ⊥ IA tại A nên OO' là tiếp tuyến của đường tròn \(\left( {I;{{DE} \over 2}} \right).\) d) Tam giác O'IO vuông tại I có IA ⊥ OO'. Theo hệ thức lượng trong tam giác vuông, ta có: IA2 = OA.O'A = 5.3,2 = 16 Suy ra: IA = 4 (cm). Mà DE = 2IA nên DE = 2.4 = 8 (cm). Sachbaitap.com
Xem lời giải SGK - Toán 9 - Xem ngay >> Học trực tuyến lớp 9 và Lộ trình UP10 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Lộ trình học tập 3 giai đoạn: Học nền tảng lớp 9, Ôn thi vào lớp 10, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
Xem thêm tại đây:
Ôn tập chương II - Đường tròn
|
-
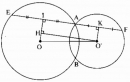
Câu 83* trang 171 Sách bài tập (SBT) Toán 9 Tập 1
Cho hai đường tròn (O) và (O') cắt nhau tại A và B, OO' = 3cm. Qua A kẻ một đường thẳng cắt các đường tròn (O) và (O') theo thứ tự tại E và F ( A nằm giữa E và F). Tính xem đoạn thẳng EF có độ dài lớn nhất bằng bao nhiêu?
-
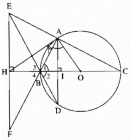
Câu 84 trang 171 Sách bài tập (SBT) Toán 9 Tập 1
Cho tam giác ABC vuông tại A ( AB < AC) nội tiếp đường tròn (O) có đường kính BC. Kẻ dây AD vuông góc với BC. Gọi E là giao điểm của DB và CA. Qua E kẻ đường thẳng vuông góc với BC, cắt BC ở H, cắt AB ở F. Chứng minh rằng:
-
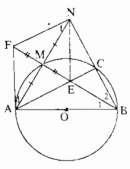
Câu 85 trang 172 Sách bài tập (SBT) Toán 9 Tập 1
Cho đường tròn (O), đường kính AB, điểm M thuộc đường tròn. Vẽ điểm N đối xứng với A qua M. BN cắt đường tròn ở C. Gọi E là giao điểm của AC và BM.
-
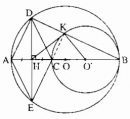
Câu 86 trang 172 Sách bài tập (SBT) Toán 9 Tập 1
Cho đường tròn (O), đường kính AB, điểm C nằm giữa A và O. Vẽ đường tròn (O) có đường kính CB.

 Tải ngay
Tải ngay