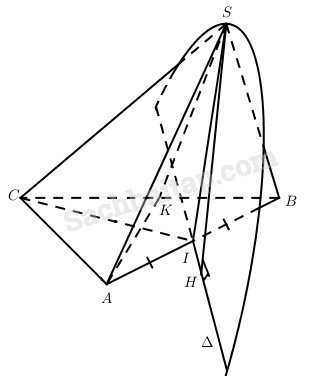
Câu 85 trang 130 Sách bài tập Hình học 11 Nâng cao

Cho ABC là tam giác cân có \(AB = AC = A,\widehat {BAC} = {120^0}\). Điểm S thay đổi trong không gian nhưng luôn ở về một phía của mặt phẳng (ABC) và \(AS = a,\widehat {SAB} = {60^0}\).

a) Gọi H là hình chiếu của điểm S trên mặt phẳng (ABC). Chứng minh rằng H thuộc đường thẳng cố định và S thuộc đường tròn cố định, tính bán kính đường tròn đó.

b) Chứng minh rằng khi độ dài SH đạt giá trị lớn nhất thì hai mặt phẳng (SAB) và (ABC) vuông góc với nhau và khi đó hãy tính độ dài SC.

c) Khi SBC là tam giác vuông tại S, hãy tính góc giữa hai đường thẳng SA với AC và khoảng cách từ A đến mặt phẳng (SBC).

Trả lời

a) Vì \(AB = a,SA = a,\widehat {SAB} = {60^0}\) nên SAB là tam giác đều, từ đó điểm S thuộc mặt phẳng trung trực (α) của AB và mặt phẳng (α) cố định, ngoài ra \((\alpha ) \bot \left( {ABC} \right)\). Kí hiệu \(\Delta  = \left( \alpha  \right) \cap \left( {ABC} \right)\) thì ∆ cố định.

Do H là hình chiếu của S trên (ABC) nên H thuộc ∆.

Vậy hình chiếu của S trên mặt phẳng (ABC) thuộc đường thẳng ∆ cố định nói trên.

Gọi I là trung điểm của AB ta có \(SI = {{a\sqrt 3 } \over 2}\), như vậy, điểm S thuộc đường tròn tâm I, bán kính \({{a\sqrt 3 } \over 2}\), trong mặt phẳng (α) nói trên, tức là điểm S thuộc đường tròn cố định.

b) Ta có \(SH \le SI = {{a\sqrt 3 } \over 2}\). Như vậy giá trị lớn nhất của SH bằng \({{a\sqrt 3 } \over 2}\) khi H trùng với điểm I.

Do \(SI \subset \left( {SAB} \right)\) và \(I \equiv H,SH \bot \left( {ABC} \right)\) nên \(\left( {SAB} \right) \bot \left( {ABC} \right)\) khi SH đạt giá trị lớn nhất

Khi đó \(S{C^2} = C{I^2} + S{I^2} = {\left( {{{a\sqrt 3 } \over 2}} \right)^2} + C{I^2}\)

Mặt khác

\(\eqalign{  & C{I^2} = C{A^2} + A{I^2} - 2{\rm{A}}C.AI.\cos {120^0}  \cr  &  = {a^2} + {{{a^2}} \over 4} + 2a.{a \over 2}.{1 \over 2} = {{7{a^2}} \over 4} \cr} \)

Từ đó \(S{C^2} = {{3{{\rm{a}}^2}} \over 4} + {{7{{\rm{a}}^2}} \over 4} = {{10{a^2}} \over 4}\)

hay \(SC = {{a\sqrt {10} } \over 2}\)

c) - Khi SBC là tam giác vuông tại điểm S thì hình chiếu của điểm A trên mp(SBC) là trung điểm K của BC.

Thật vậy, ta có \(AS = AC = AB\) nên \(K{\rm{S}} = KC = KB\) .

Do đó, AK là khoảng cách từ điểm A đến mp(SBC).

Dễ thấy \(AK = AC\cos {60^0} = {a \over 2}\)

- Vì \(BC = a\sqrt 3 ,SB = a\) nên \(SC = a\sqrt 2 \)

Mặt khác \(SA = AC = a\) nên \(S{C^2} = A{S^2} + A{C^2}\), tức là \(\widehat {SAC} = {90^0}\)

Như vậy, góc giữa hai đường thẳng SA và AC bằng 90°.

Sachbaitap.com