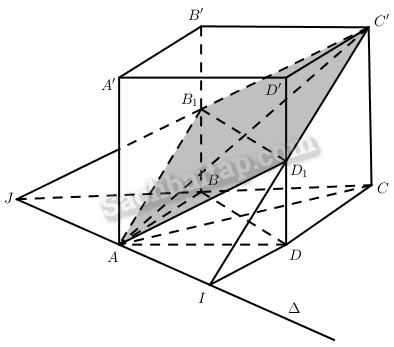
Câu 86 trang 131 Sách bài tập Hình học 11 Nâng caoGiải bài tập Câu 86 trang 131 Sách bài tập Hình học 11 Nâng cao Cho hình lăng trụ tứ giác đều ABCD.A’B’C’D’ cạnh đáy bằng a, cạnh bên \(a\sqrt 6 \). Xét đường thẳng ∆ đi qua điểm A và song song với BD. Gọi (P) là mặt phẳng qua ∆ và điểm C’. a) Thiết diện của hình lăng trụ đã cho khi cắt bởi mp(P) là hình gì? Tính diện tích thiết diện. b) Tính góc giữa mp(P) và mp(ABCD). Trả lời
a) Gọi \(I = C{\rm{D}} \cap \Delta ,J = BC \cap \Delta \), \({B_1} = C'J \cap BB',{D_1} = C'I \cap {\rm{DD}}'\) thì thiết diện thu được \(A{B_1}C'{D_1}\). Dễ thấy \(A{B_1}C'{D_1}\) là hình bình hành và B1, D1 lần lượt là trung điểm của BB’, DD’. Từ đó \(A{{\rm{D}}_1} = {D_1}C'\) Do đó thiết diện \(A{B_1}C'{D_1}\) là hình thoi. \(\eqalign{ & {S_{A{B_1}C'{D_1}}} = {1 \over 2}{B_1}{D_1},AC' \cr & {B_1}{D_1} = B{\rm{D}} = a\sqrt 2 \cr & AC{'^2} = A{C^2} + CC{'^2} = 2{{\rm{a}}^2} + 6{{\rm{a}}^2} = 8{{\rm{a}}^2} \cr & \Rightarrow AC' = 2{\rm{a}}\sqrt 2 \cr} \) Vậy \({S_{A{B_1}C'{D_1}}} = {1 \over 2}a\sqrt 2 .2{\rm{a}}\sqrt 2 = 2{{\rm{a}}^2}.\) b) Ta có \(AC \bot B{\rm{D}}\) mà ∆ // BD nên \(AC \bot \Delta \). Mặt khác \(C'C \bot \left( {ABC{\rm{D}}} \right)\) nên \(AC' \bot \Delta \) (định lí ba đường vuông góc). Vậy \(\widehat {C'AC}\) là góc giữa mp(P) và mp(ABCD). Ta có \(\tan \widehat {C'AC} = {{CC'} \over {AC}} = {{a\sqrt 6 } \over {a\sqrt 2 }} = \sqrt 3 \), từ đó \(\widehat {C'AC} = {60^0}\) Chú ý. Cũng có thể tính góc giữa mp(P) và mp(ABCD) bởi công thức \({S_{ABC{\rm{D}}}} = {S_{A{B_1}C'{D_1}}} = 2{{\rm{a}}^2}\) mà \({S_{ABC{\rm{D}}}} = {a^2},{S_{A{B_1}C'{D_1}}} = 2{{\rm{a}}^2}\) tức là \(\cos \varphi = {1 \over 2}\,\,hay\,\,\varphi = {60^0}\). Sachbaitap.com
Xem lời giải SGK - Toán 11 Nâng cao - Xem ngay >> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
Xem thêm tại đây:
Ôn tập chương III. Vectơ trong không gian. Quan hệ vuông góc
|
-
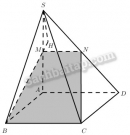
Câu 87 trang 131 Sách bài tập Hình học 11 Nâng cao
Giải bài tập Câu 87 trang 131 Sách bài tập Hình học 11 Nâng cao
-
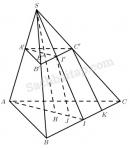
Câu 88 trang 131 Sách bài tập Hình học 11 Nâng cao
Giải bài tập Câu 88 trang 131 Sách bài tập Hình học 11 Nâng cao
-
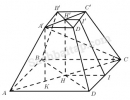
Câu 89 trang 131 Sách bài tập Hình học 11 Nâng cao
Giải bài tập Câu 89 trang 131 Sách bài tập Hình học 11 Nâng cao
-

Câu 1, 2, 3, 4, 5, 6 trang 131, 132 Sách bài tập Hình học 11 Nâng cao
Giải bài tập Câu 1, 2, 3, 4, 5, 6 trang 131, 132 Sách bài tập Hình học 11 Nâng cao

 Tải ngay
Tải ngay