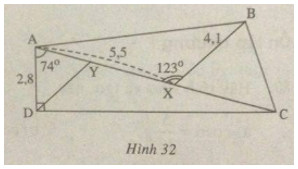
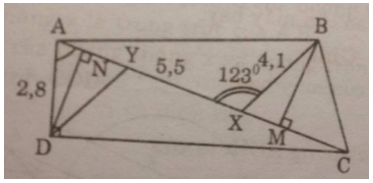
Câu 86 trang 120 Sách Bài Tập (SBT) Toán 9 Tập 1Tính diện tích tam giác Cho hình 32.
Biết: \(AD \bot DC,\widehat {DAC} = 74^\circ \) \(\widehat {AXB} = 123^\circ ,AD = 2,8\,cm\) AX = 5,5cm, BX = 4,1cm. a) Tính AC. b) Gọi Y là điểm trên AX sao cho DY ⁄⁄ BX. Hãy tính XY c) Tính diện tích tam giác BCX Gợi ý làm bài a) Trong tam giác vuông ACD, ta có: \(AC = {{AD} \over {\cos \widehat {CAD}}} = {{2,8} \over {\cos 74^\circ }} \approx 10,158\,(cm)\) b) Kẻ \(DN \bot AC\) Trong tam giác vuông AND, ta có: \(\eqalign{ \(\eqalign{ Vì BX // DY nên \(\widehat {D{\rm{YX}}} = \widehat {BXY} = 123^\circ \) ( hai góc so le trong) Mà \(\widehat {DYN} + \widehat {D{\rm{YX}}} = 180^\circ \) (kề bù) Suy ra: \(\widehat {DYN} = 180^\circ - \widehat {D{\rm{YX}}} = 180^\circ - 123^\circ = 57^\circ \) Trong tam giác vuông DYN, ta có: \(\eqalign{ Ta có: \(\eqalign{
c) Ta có: \(CX = AC - AX \approx 10,158 - 5,5 = 4,658\,(cm)\) Kẻ \(BM \bot CX\) Ta có: \(\widehat {BXC} = 180^\circ - \widehat {BXA} = 180^\circ - 123^\circ = 57^\circ \) Trong tam giác vuông BMX, ta có: \(\eqalign{ \(\eqalign{ Sachbaitap.com
Xem lời giải SGK - Toán 9 - Xem ngay >> Học trực tuyến lớp 9 và Lộ trình UP10 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Lộ trình học tập 3 giai đoạn: Học nền tảng lớp 9, Ôn thi vào lớp 10, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
Xem thêm tại đây:
Ôn tập chương I - Hệ thức lượng trong tam giác vuông
|
-
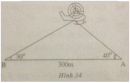
Câu 88 trang 121 Sách Bài Tập (SBT) Toán 9 Tập 1
Điểm hạ cánh của một máy bay trực thăng ở giữa hai người quan sát A và B
-
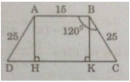
Câu 89 trang 121 Sách Bài Tập (SBT) Toán 9 Tập 1
Cho hình thang với đáy nhỏ là 15cm, hai cạnh bên bằng nhau và bằng 25cm
-
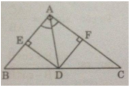
Câu 90 trang 121 Sách Bài Tập (SBT) Toán 9 Tập 1
Cho tam giác ABC vuông tại A, AB = 6cm, AC = 8cm

 Tải ngay
Tải ngay