Các mục con
-
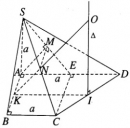
Bài 2.21 trang 64 sách bài tập (SBT) – Hình học 12
Hình chóp S.ABCD có SA = a là chiều cao của hình chóp và đáy ABCD là hình thang vuông tại A và B có AB = BC = a và AD = 2a. Gọi E là trung điểm của cạnh AD. Xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp S.CDE
-
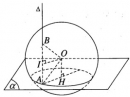
Bài 2.22 trang 64 sách bài tập (SBT) – Hình học 12
Cho hình cầu tâm O bán kính r. Lấy một điểm A trên mặt cầu và gọi là mặt phẳng đi qua A sao cho góc giữa OA và bằng 300.
-
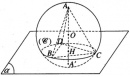
Bài 2.23 trang 64 sách bài tập (SBT) – Hình học 12
Cho hình cầu đường kính AA’ = 2r. Gọi H là một điểm trên đoạn AA’ sao cho . Mặt phẳng qua H và vuông góc với AA’ cắt hình cầu theo đường tròn (C).
-
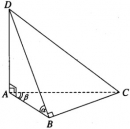
Bài 2.24 trang 65 sách bài tập (SBT) – Hình học 12
Cho tứ diện ABCD có và . Khi quay tất cả các cạnh của tứ diện đó quanh cạnh AB có những hình nón nào được tạo thành ? Hãy kể tên các hình nón đó.
-
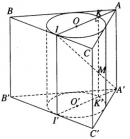
Bài 2.25 trang 65 sách bài tập (SBT) – Hình học 12
Cho lăng trụ tam giác đều ABC.A’B’C’ có cạnh đáy bằng a và có đường cao h.
-
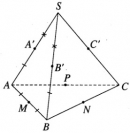
Bài 2.26 trang 65 sách bài tập (SBT) – Hình học 12
Cho hình chóp S.ABC và biết rằng có một mặt cầu tiếp xúc với tất cả các cạnh bên của hình chóp đồng thời tiếp xúc với ba cạnh của đáy tại trung điểm của mỗi cạnh đáy. Chứng minh hình chóp đó là hình chóp đều.
-
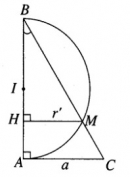
Bài 2.27 trang 65 sách bài tập (SBT) – Hình học 12
Trong mặt phẳng a, cho tam giác ABC vuông tại A có cạnh AC = a và có cạnh huyền BC = 2a. Cũng trong mặt phẳng đó cho nửa đường tròn đường kính AB cắt cạnh BC tại M.
-
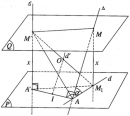
Bài 2.28 trang 65 sách bài tập (SBT) – Hình học 12
Mặt phẳng (Q) song song với mặt phẳng (P) cắt ∆ và ∆' lần lượt tại M và M’. Gọi M1 là hình chiếu vuông góc của M lên mặt phẳng (P).
-
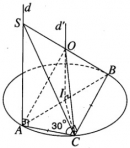
Bài 2.29 trang 66 sách bài tập (SBT) – Hình học 12.
Cho tam giác vuông cân ABC có cạnh huyền AB = 2a. Trên đường thẳng d đi qua A và vuông góc với mặt phẳng (ABC), lấy một điểm S khác A, ta được tứ diện SABC.
-
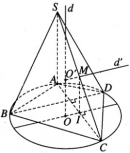
Bài 2.30 trang 66 sách bài tập (SBT) – Hình học 12.
Cho đường tròn tâm O bán kính r’. Xét hình chóp S.ABCD có SA vuông góc với mặt phẳng đáy, S và A cố định, SA = h cho trước và có đáy ABCD là một tứ giác tùy ý nội tiếp đường tròn đã cho, trong đó các đường chéo AC và BD vuông góc với nhau.
-
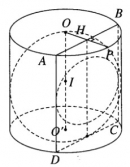
Bài 2.32 trang 66 sách bài tập (SBT) – Hình học 12.
Hình trụ tròn xoay có bán kính đáy bằng r, có chiều cao bằng 2r và có trục là OO’.
-
Đề 1 trang 67 Sách bài tập (SBT) Hình học 12
Cho hình nón (H) có chiều cao bằng h, đường sinh tạo với mặt phẳng đáy một góc bằng 600. a) Tính thể tích khối nón (H)
-
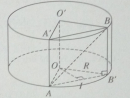
Đề 2 trang 67 Sách bài tập (SBT) Hình học 12
Cho hình trụ (H) có đáy là hai đường tròn tâm O và O’ , bán kính đáy R = OO’. Trên đáy tâm O lấy điểm A, trên đáy tâm O’ lấy điểm B sao cho AB = 2R. Tính tỉ số thể tích giữa khối tứ diện ABOO’ và khối trụ (H).
-
Đề 3 trang 67 Sách bài tập (SBT) Hình học 12
Cho ba điểm A, B, C nằm trên mặt cầu (S) tâm O, AB = 5a , AC = 4a , BC = 3a , khoảng cách từ O đến mặt phẳng (ABC) bằng 2a. Tính thể tích mặt cầu (S) theo a.

 Tải ngay
Tải ngay