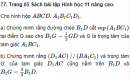-
Bài 68 trang 63 SBT Hình học 11 nâng cao.
Chứng minh rằng nếu n đường thẳng đôi một cắt nhau và không đồng phẳng thì chúng đồng quy.
-

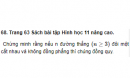
Câu 69 trang 63 Sách bài tập Hình học 11 nâng cao.
Gọi E là giao điểm của AD và BC; M là trung điểm của AB; G là trọng tâm của tam giác ECD.
-

Câu 70 trang 63 Sách bài tập Hình học 11 nâng cao.
Trong mp(P) cho hai đường thẳng a và b cắt nhau tại O.
-

Câu 71 trang 64 Sách bài tập Hình học 11 nâng cao.
Cho hình chóp S.ABCD có đáy là một tứ giác lồi. Gọi M, I, J, O lần lượt là trung điểm của SD, AB, CD, IJ.
-

Câu 72 trang 64 Sách bài tập Hình học 11 nâng cao.
Cho hình chóp S.ABCD và một điểm M nằm trong tam giác ABC.
-

Câu 75 trang 65 Sách bài tập Hình học 11 nâng cao.
Cho hình chóp S.ABCD có đáy là một tứ giác lồi. Gọi O là giao điểm của hai đường chéo AC và BD; M là trung điểm của cạnh SA.
-

Câu 76 trang 65 Sách bài tập Hình học 11 nâng cao.
Gọi M, N, E lần lượt là trung điểm của AB, CD, SA.
-

Bài tập trắc nghiệm chương II - Đường thẳng và mặt phẳng trong không gian. Quan hệ song song
Trong các mệnh đề sau, mệnh đề nào đúng?

 Tải ngay
Tải ngay