Các mục con
-

Bài 1.28 trang 22 sách bài tập (SBT) – Hình học 12
Hình được tạo thành từ hình lập phương ABCD.A’B’C’D’ khi ta bỏ đi các điểm trong của mặt phẳng (ABCD) có phải là một hình đa diện không?
-

Bài 1.29 trang 22 sách bài tập (SBT) – Hình học 12
Chứng minh rằng mỗi đỉnh của một hình đa diện là đỉnh chung của ít nhất ba cạnh.
-
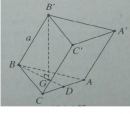
Bài 1.30 trang 22 sách bài tập (SBT) – Hình học 12
Cho hình lăng trị ABC.A’B’C’ có đáy là tam giác vuông cân ở C. Cạnh B’B = a và tạo với đáy một góc bằng 600. Hình chiếu vuông góc hạ từ B’ lên đáy trùng với trọng tâm của tam giác ABC. Tính thể tích khối lăng trụ đó theo a.
-

Bài 1.31 trang 22 sách bài tập (SBT) – Hình học 12
Tính thể tích khối lăng trụ có chiều cao bằng h, đáy là ngũ giác đều nội tiếp trong một đường tròn bán kính r.
-
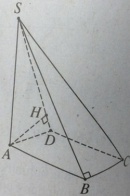
Bài 1.32 trang 22 sách bài tập (SBT) – Hình học 12
Cho hình chóp S.ABCD có đáy là hình chữ nhật ABCD, các mặt (SAB) và (SAD) vuông góc với đáy. Góc giữa mặt (SAC) và đáy bằng 600, AB = 2a , BC = a. Tính thể tích khối chóp S.ABCD và khoảng cách giữa hai đường thẳng AB và SC theo a.
-
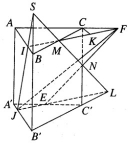
Bài 1.33 trang 22 sách bài tập (SBT) – Hình học 12
Cho lăng trụ đứng ABC.A’B’C’ có đáy là tam giác đều cạnh bằng a. Gọi M, N và E theo thứ tự là trung điểm của BC, CC’ và C’A’. Đường thẳng EN cắt đường thẳng AC tại F, đường thẳng MN cắt đường thẳng B’C’ tại L. Đường thẳng FM kéo dài cắt AB tại I, đường thẳng LE kéo dài cắt A’B’ tại J.
-
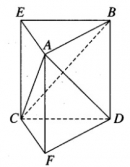
Bài 1.34 trang 22 sách bài tập (SBT) – Hình học 12
Cho hai đoạn thẳng AB và CD chéo nhau, AC là đường vuông góc chung của chúng. Biết rằng AC = h, AB = a, CD = b và góc giữa hai đường thẳng AB và CD bằng 600. Hãy tính thể tích của khối tứ diện ABCD.
-

Bài 1.35 trang 22 sách bài tập (SBT) – Hình học 12
Cho tứ diện đều ABCD. Gọi (H) là hình bát diện đều có các đỉnh là trung điểm các cạnh của tứ diện đều đó. Tính tỉ số .
-
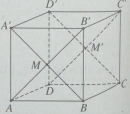
Đề 1 trang 23 Sách bài tập (SBT) Hình học 12
Cho hình lập phương ABCD. A’B’C’D’. Chứng minh hai tứ diện ABCB’ và AA’D’B’ bằng nhau.
-
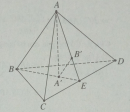
Đề 2 trang 23 Sách bài tập (SBT) Hình học 12
Cho khối tứ diện đều ABCD cạnh bằng a. Gọi A’, B’ , C’ , D’ lần lượt là trọng tâm của các tam giác BCD , CDA , DAB , ABC.
-
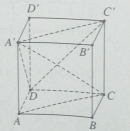
Bài 1.36 trang 23 sách bài tập (SBT) – Hình học 12
Cho hình lập phương ABCD.A’B’C’D’ cạnh a, M là trung điểm của BB’ Tính theo a :
-
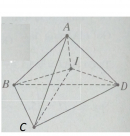
Bài 1.37 trang 23 sách bài tập (SBT) – Hình học 12
Cho tứ diện ABCD. Gọi hA , hB, hC, hD lần lượt là các đường cao của tứ diện xuất phát từ A, B, C, D và r là bán kính mặt cầu nội tiếp tứ diện. Chứng minh rằng:
-
Đề 3 trang 24 Sách bài tập (SBT) Hình học 12
Cho khối hộp ABCD.A’B’C’D’ có thể tích bằng V, I là giao điểm các đường chéo của nó. Mặt phẳng (P) đi qua I và cắt các cạnh bên của khối hộp chia khối hộp đó thành hai khối đa diện. Tính thể tích của mỗi khối đa diện đó theo V.

 Tải ngay
Tải ngay