Các mục con
-

Câu 2.41 trang 67 sách bài tập Đại số và Giải tích 11 Nâng cao
Một hộp đựng 9 thẻ được đánh số 1, 2,…9. Rút ngẫu nhiên hai thẻ và nhân hai số ghi trên hai thẻ với nhau. Tính xác suất để a) Tích nhận được là số lẻ. b) Tích nhận được là số chẵn.
-

Câu 2.42 trang 67 sách bài tập Đại số và Giải tích 11 Nâng cao
Một hộp đựng 9 thẻ được số 1, 2, ….9. Rút ngẫu nhiên 5 thẻ. Tính xác suất để a) Các thẻ ghi số 1, 2, 3 được rút. b) Có đúng một trong ba thẻ ghi số 1, 2, 3 được rút. c) Không thẻ nào trong ba thẻ ghi các số 1, 2, 2 được rút.
-

Câu 2.43 trang 67 sách bài tập Đại số và Giải tích 11 Nâng cao
Tám người trong đó có hai vợ chồng anh A được xếp ngẫu nhiên xung quanh một bàn tròn. Tính xác suất để hai vợ chồng anh A ngồi cạnh nhau (cách sắp xếp được hiểu như bài 2.19).
-

Câu 2.45 trang 67 sách bài tập Đại số và Giải tích 11 Nâng cao
Chọn ngẫu nhiên một vé xổ số có 2 chữ số từ 0 đến 9. Tính xác suất để số trên vé không có chữ số 1 hoặc không có chữ số 5.
-

Câu 2.46 trang 67 sách bài tập Đại số và Giải tích 11 Nâng cao
Một người say rượu bước bốn bước. Mỗi bước anh ta tiến lên phía trước nửa mét hoặc lùi lại phía sau nửa mét với xác suất như nhau. Tính xác suất để sau bốn bước đó anh ta trở lại điểm xuất phát.
-
Câu 2.47 trang 68 sách bài tập Đại số và Giải tích 11 Nâng cao
Chọn ngẫu nhiên 3 người, biết rằng không có ai sinh vào năm nhuận. Hãy tính xác suất để có ít nhất hai người có sinh nhật trùng nhau (cùng ngày, cùng tháng).
-

Câu 2.48 trang 68 sách bài tập Đại số và Giải tích 11 Nâng cao
Một người đi du lịch mang ba hộp thịt, 2 hộp hoa quả và 3 hộp sữa. Do trời mưa nên các hộp thịt mất nhãn. Người đó chọn ngẫu nhiên ba hộp. Tính xác suất để trong đó có một hộp thịt, một hộp sữa, một hộp hoa quả.
-

Câu 2.49 trang 68 sách bài tập Đại số và Giải tích 11 Nâng cao
Trong danh sách 10 đường phố cần tu sửa ở Hà Nội, có 2 đường thuộc quận Hoàn Kiếm, 4 đường thuộc quận Ba Đình, 4 đường thuộc quận Đống Đa.
-

Câu 2.50 trang 68 sách bài tập Đại số và Giải tích 11 Nâng cao
Gieo một con súc sắc cân đối ba lần. Gọi X là số lần con súc sắc xuất hiện mặt 6 chấm. a) Lập bảng phân bố xác suất của X.
-

Câu 2.51 trang 68 sách bài tập Đại số và Giải tích 11 Nâng cao
Xác suất bắn trúng vòng 10 của An là 0,4. An bắn 3 lần. Gọi X là số lần trúng vòng 10. a) Lập bảng phân bố xác suất của X.
-
Câu 2.52 trang 68 sách bài tập Đại số và Giải tích 11 Nâng cao
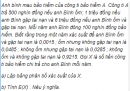
Anh Bình mua bảo hiểm của công ty bảo hiểm A. Công ty A trả 500 nghìn đồng nếu anh Bình ốm; 1 triệu đồng nếu anh Bình gặp tai nạn và 6 triệu đồng nếu anh Bình ốm và gặp tai nạn.
-

Câu 2.53 trang 69 sách bài tập Đại số và Giải tích 11 Nâng cao
Bố của An đề nghị thưởng cho An 90 000 đồng để mua một vật kỉ niệm nào đó, nếu An được điểm giỏi ở cả bốn môn học: Toán, Ngoại ngữ, Tin học, Tiếng việt
-

Câu 2.54 trang 69 sách bài tập Đại số và Giải tích 11 Nâng cao
Một bộ ghép hình gồm các miếng gỗ. Mỗi miếng gỗ được đặc trưng bởi 4 tiêu chuẩn: chất liệu, màu sắc, hình dạng và kích cỡ.
-

Câu 2.55 trang 69 sách bài tập Đại số và Giải tích 11 Nâng cao
Tại một buổi lễ có 13 cặp vợ chồng tham dự. Mỗi ông bắt tay một lần với mọi người trừ vợ mình. Các bà không ai bắt tay với nhau. Hỏi có bao nhiêu cái bắt tay? (A) 78 (B) 185 (C) 234 (D) 312
-

Câu 2.56 trang 69 sách bài tập Đại số và Giải tích 11 Nâng cao
Trong các số tự nhiên từ 100 đến 999 có bao nhiêu số mà các chữ số của nó tăng dần hoặc giảm dần?
-
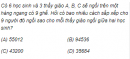
Câu 2.57 trang 70 sách bài tập Đại số và Giải tích 11 Nâng cao
Có 6 học sinh và 3 thầy giáo A, B, C sẽ ngồi trên một hàng ngang có 9 ghế.
-

Câu 2.58 trang 70 sách bài tập Đại số và Giải tích 11 Nâng cao
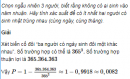
Một hộp đựng 11 tấm thẻ được đánh số từ 1 đến 11. Chọn ngẫu nhiên 6 tấm thẻ. Gọi P là xác suất để tổng số ghi trên 6 tấm thẻ ấy là một số lẻ. Khi đó P bằng
-

Câu 2.59 trang 70 sách bài tập Đại số và Giải tích 11 Nâng cao
Chọn ngẫu nhiên 6 số nguyên dương trong tập [1, 2, 3,…,10] và sắp xếp chúng theo thứ tự tăng dần (từ thấp lên cao). Gọi P là xác suất để số 3 được chọn và xếp ở vị trí thứ hai.
-
Câu 2.60 trang 70 sách bài tập Đại số và Giải tích 11 Nâng cao
Có ba chiếc hộp A, B, C mỗi hộp chứa ba chiếc thẻ được đánh số 1, 2, 3. Từ mỗi hộp rút ngẫu nhiên một chiếc thẻ. Gọi P là xác suất để tổng số ghi trên ba tấm thẻ là 6. Khi đó P bằng:

 Tải ngay
Tải ngay