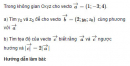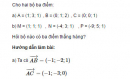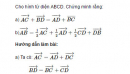Các mục con
-
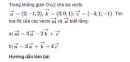
Bài 3.1 trang 102 sách bài tập (SBT) – Hình học 12
Trong không gian Oxyz cho ba vecto . Tìm tọa độ của các vecto và biết rằng:
-
Bài 3.3 trang 102 sách bài tập (SBT) – Hình học 12
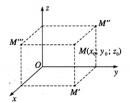
Trong không gian Oxyz cho điểm M có tọa độ (x0; y0 ; z0). Tìm tọa độ hình chiếu vuông góc của điểm M trên các mặt phẳng tọa độ (Oxy), (Oyz), (Ozx).
-
Bài 3.5 trang 102 sách bài tập (SBT) – Hình học 12
Trong không gian Oxyz, hãy tìm trên mặt phẳng (Oxz) một điểm M cách đều ba điểm A(1; 1; 1), B(-1; 1; 0), C(3; 1; -1).
-
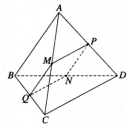
Bài 3.7 trang 102 sách bài tập (SBT) – Hình học 12
Cho hình tứ diện ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AC, BD, AD, BC. Chứng minh rằng:
-
Bài 3.8 trang 102 sách bài tập (SBT) – Hình học 12
Trong không gian cho ba vecto tùy ý . Gọi . Chứng tỏ rằng ba vecto đồng phẳng.
-
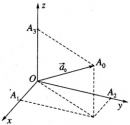
Bài 3.9 trang 103 sách bài tập (SBT) – Hình học 12
Trong không gian Oxyz cho một vecto tùy ý khác vecto . Gọi là ba góc tạo bởi ba vecto đơn vị trên ba trục Ox, Oy, Oz và vecto . Chứng minh rằng:
-
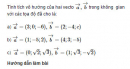
Bài 3.11 trang 103 sách bài tập (SBT) – Hình học 12
Tính tích vô hướng của hai vecto trong không gian với các tọa độ đã cho là:
-

Bài 3.12 trang 103 sách bài tập (SBT) – Hình học 12
Tính khoảng cách giữa hai điểm A và B trong mỗi trường hợp sau:
-

Bài 3.13 trang 103 sách bài tập (SBT) – Hình học 12
Trong không gian Oxyz cho tam giác ABC có tọa độ các đỉnh là:
-

Bài 3.14 trang 103 sách bài tập (SBT) – Hình học 12
Trong không gian Oxyz hãy lập phương trình mặt cầu trong các trường hợp sau:
-
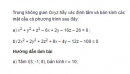
Bài 3.15 trang 103 sách bài tập (SBT) – Hình học 12
Trong không gian Oxyz hãy xác định tâm và bán kính các mặt cầu có phương trình sau đây:
-

Bài 3.16 trang 103 sách bài tập (SBT) – Hình học 12
Trong không gian Oxyz hãy viết phương trình mặt cầu đi qua bốn điểm A(1; 0; 0), B(0; -2; 0), C(0; 0; 4) và gốc tọa độ O. Hãy xác định tâm và bán kính của mặt cầu đó.
-

Bài 3.17 trang 113 sách bài tập (SBT) – Hình học 12
Viết phương trình mặt phẳng trong các trường hợp sau:
-

Bài 3.18 trang 113 sách bài tập (SBT) – Hình học 12
Viết phương trình mặt phẳng trung trực của đoạn thẳng AB với A(1; -2; 4), B(3; 6; 2).
-

Bài 3.19 trang 113 sách bài tập (SBT) – Hình học 12
Cho tứ diện có các đỉnh là A(5; 1; 3), B(1; 6; 2), C(5; 0 ; 4), D(4; 0 ; 6)
-
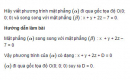
Bài 3.20 trang 113 sách bài tập (SBT) – Hình học 12
Hãy viết phương trình mặt phẳng đi qua gốc tọa độ O(0; 0; 0) và song song với mặt phẳng : x + y + 2z – 7 = 0.

 Tải ngay
Tải ngay