-

Bài 3.17 trang 113 sách bài tập (SBT) – Hình học 12
Viết phương trình mặt phẳng trong các trường hợp sau:
-

Bài 3.18 trang 113 sách bài tập (SBT) – Hình học 12
Viết phương trình mặt phẳng trung trực của đoạn thẳng AB với A(1; -2; 4), B(3; 6; 2).
-

Bài 3.19 trang 113 sách bài tập (SBT) – Hình học 12
Cho tứ diện có các đỉnh là A(5; 1; 3), B(1; 6; 2), C(5; 0 ; 4), D(4; 0 ; 6)
-
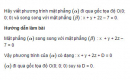
Bài 3.20 trang 113 sách bài tập (SBT) – Hình học 12
Hãy viết phương trình mặt phẳng đi qua gốc tọa độ O(0; 0; 0) và song song với mặt phẳng : x + y + 2z – 7 = 0.
-

Bài 3.21 trang 113 sách bài tập (SBT) – Hình học 12
Lập phương trình mặt phẳng đi qua hai điểm A(0; 1; 0) , B(2; 3; 1) và vuông góc với mặt phẳng : x + 2y – z = 0 .
-
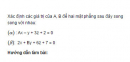
Bài 3.22 trang 114 sách bài tập (SBT) – Hình học 12
Xác định các giá trị của A, B để hai mặt phẳng sau đây song song với nhau:
-
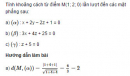
Bài 3.23 trang 114 sách bài tập (SBT) – Hình học 12
Tính khoảng cách từ điểm M(1; 2; 0) lần lượt đến các mặt phẳng sau:
-

Bài 3.25 trang 114 sách bài tập (SBT) – Hình học 12
Cho hình lập phương ABCD. A’B’C’D’ có cạnh bằng 1. Dùng phương pháp tọa độ để:
-
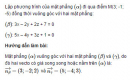
Bài 3.26 trang 114 sách bài tập (SBT) – Hình học 12
Lập phương trình của mặt phẳng đi qua điểm M(3; -1; -5) đồng thời vuông góc với hai mặt phẳng:
-

Bài 3.27 trang 114 sách bài tập (SBT) – Hình học 12
Cho điểm A(2; 3; 4). Hãy viết phương trình của mặt phẳng đi qua các hình chiếu của điểm A trên các trục tọa độ.
-
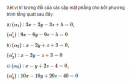
Bài 3.28 trang 114 sách bài tập (SBT) – Hình học 12
Xét vị trí tương đối của các cặp mặt phẳng cho bởi phương trình tổng quát sau đây:
-

Bài 3.29 trang 114 sách bài tập (SBT) – Hình học 12
Viết phương trình của mặt phẳng đi qua điểm M(2; -1; 2), song song với trục Oy và vuông góc với mặt phẳng : 2x – y + 3z + 4 = 0
-
Bài 3.30 trang 114 sách bài tập (SBT) – Hình học 12
Lập phương trình của mặt phẳng đi qua điểm M(1; 2; 3) và cắt ba tia Ox, Oy, Oz lần lượt tại A, B, C sao cho thể tích tứ diện OABC nhỏ nhất.

 Tải ngay
Tải ngay
