-
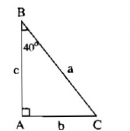
Câu 21. Trang 106 Sách Bài Tập (SBT) Toán 9 Tập 1
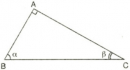
Vẽ một tam giác vuôg có một góc nhon bằng rồi viết các tỉ số lượng giác của góc . Giải:
-
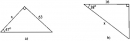
Câu 25. Trang 107 Sách Bài Tập (SBT) Toán 9 Tập 1
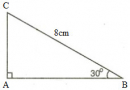
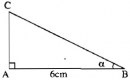
Tìm giá trị x (làm tròn đến chữ số thập phân thứ ba) trong mỗi tam giác vuông với kích thước được chỉ ra trên hình 10, biết rằng:
-
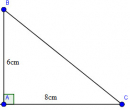
Câu 26. Trang 107 Sách Bài Tập (SBT) Toán 9 Tập 1
Cho tam giác ABC vuông tại A, trong đó AB = 6cm, AC = 8cm. Tính các tỉ số lượng giác của góc B, từ đó suy ra các tỉ số lượng giác của góc C.
-
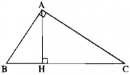
Câu 27. Trang 107 Sách Bài Tập (SBT) Toán 9 Tập 1
Cho tam giác ABC vuông tại A. Kẻ đường cao AH. Tính sinB, sinC trong mỗi trường hợp sau (làm tròn đến chữ số thập phân thứ tư), biết rằng:
-

Câu 28. Trang 107 Sách Bài Tập (SBT) Toán 9 Tập 1
Hãy biến đổi các tỉ số lượng giác sau đây thành tỉ số lượng giác của các góc nhỏ hơn 45°
-

Câu 29. Trang 107 Sách Bài Tập (SBT) Toán 9 Tập 1
Xét quan hệ giữa hai góc trong mỗi biểu thức rồi tính:
-
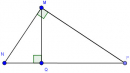
Câu 30. Trang 107 Sách Bài Tập (SBT) Toán 9 Tập 1
Đường cao MQ của tam giác vuông MNP chia cạnh huyền NP thành hai đoạn NQ = 3, PQ = 6. Hãy so sánh cotgN và cotgP. Tỉ số nào lớn hơn và lớn hơn bao nhiêu lần?
-
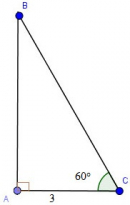
Câu 31. Trang 108 Sách Bài Tập (SBT) Toán 9 Tập 1
Cạnh góc vuông kề với góc của một tam giác vuông bằng 3. Sử dụng bằng lượng giác của các góc đặc biệt, hãy tìm cạnh huyền và cạnh góc vuông còn lại (làm tròn đến chữ số thập phân thứ tư).
-
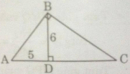
Câu 32. Trang 108 Sách Bài Tập (SBT) Toán 9 Tập 1
Đường cao BD của tam giác nhọn ABC bằng 6, đoạn thẳng AD = 5.
-

Câu 34. Trang 108 Sách Bài Tập (SBT) Toán 9 Tập 1
Hãy tìm sin a, cos a (làm tròn đến chữ số thập phân thứ tư) nếu biết:
-
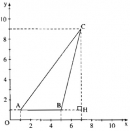
Câu 36. Trang 108 Sách Bài Tập (SBT) Toán 9 Tập 1
Trong mặt phẳng tọa độ, các đỉnh của tam giác ABC có tọa độ như sau: A(1 ; 1) ; B(5 ; 1) ; C(7 ; 9)
-
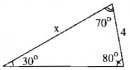
Câu 37. Trang 108 Sách Bài Tập (SBT) Toán 9 Tập 1
Hãy viết một phương trình để từ đó có thể tìm được x (không phải giải phương trình này).
-
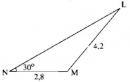
Câu 38. Trang 108 Sách Bài Tập (SBT) Toán 9 Tập 1
Hãy tính sinL (làm tròn đến chữ số thập phân thứ tư), biết rằng
-
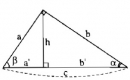
Câu 2.1, 2.2, 2.3, 2.4, 2.5, 2.6, 2.7, 2.8, 2.9, 2.10, 2.11 trang 109 Sách bài tập (SBT) Toán 9 tập 1
Tìm đẳng thức đúng trong các bài từ 2.1 đến 2.11.

 Tải ngay
Tải ngay