-
Câu 25 trang 160 Sách bài tập (SBT) Toán 9 Tập 1
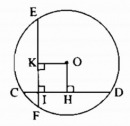
Cho hình 75, trong đó hai dây CD, EF bằng nhau và vuông góc với nhau tại I, IC = 2cm, ID = 14cm. Tính khoảng cách từ O đến mỗi dây.
-
Câu 26 trang 160 Sách bài tập (SBT) Toán 9 Tập 1
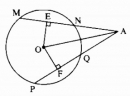
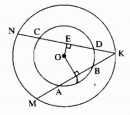
Cho đường tròn (O), dây AB và dây CD, AB < CD. Giao điểm K của các đường thẳng AB, CD nằm ngoài đường tròn. Đường tròn (O ; OK) cắt KA và KC tại M và N. Chứng minh rằng KM < KN.
-
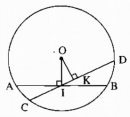
Câu 27 trang 160 Sách bài tập (SBT) Toán 9 Tập 1
Cho đường tròn (O) và điểm I nằm bên trong đường tròn. Chứng minh rằng dây AB vuông góc với OI tại I ngắn hơn mọi dây khác đi qua I.
-
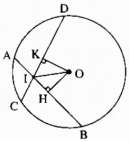
Câu 29 trang 161 Sách bài tập (SBT) Toán 9 Tập 1
Cho đường tròn (O), hai dây AB, CD bằng nhau và cắt nhau tại điểm I nằm bên trong đường tròn. Chứng minh rằng:
-
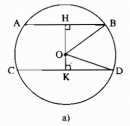
Câu 30 trang 161 Sách bài tập (SBT) Toán 9 Tập 1
Cho đường tròn tâm O bán kính 25cm. Hai dây AB, CD song song với nhau và có độ dài theo thứ tự bằng 40cm, 48cm. Tính khoảng cách giữa hai dây ấy.
-
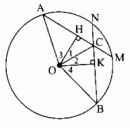
Câu 31 trang 161 Sách bài tập (SBT) Toán 9 Tập 1
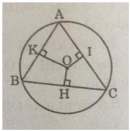
Cho đường tròn (O), các bán kính OA và OB. Trên cung nhỏ AB lấy các điểm M và N sao cho AM = BN. Gọi C là giao điểm của các đường thẳng AM và BN. Chứng minh rằng:
-
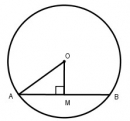
Câu 32* trang 161 Sách bài tập (SBT) Toán 9 Tập 1
Cho đường tròn tâm O bán kính 5dm, điểm M cách O là 3dm.
-
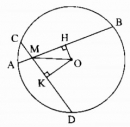
Câu 33* trang 161 Sách bài tập (SBT) Toán 9 Tập 1
Cho đường tròn (O), hai dây AB và CD cắt nhau tại điểm M nằm bên trong đường tròn. Gọi H và K theo thứ tự là trung điểm của AB và CD. Cho biết AB >CD, chứng minh rằng MH > MK.
-
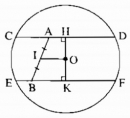
Câu 34* trang 161 Sách bài tập (SBT) Toán 9 Tập 1
Cho đường tròn (O) và hai điểm A, B nằm bên trong đường tròn và không cùng thuộc một đường kính. Dựng hai dây song song và bằng nhau sao cho điểm A nằm trên một dây, điểm B nằm trên dây còn lại.
-

Câu 3.1 Trang 161 Sách bài tập (SBT) Toán lớp 9 Tập 1
Cho đường tròn (O) đường kính 6cm, dây AB bằng 2cm. Khoảng cách từ O đến AB bằng:
-
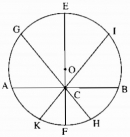
Câu 3.3* trang 161 Sách bài tập (SBT) Toán lớp 9 Tập 1
Cho đường tròn (O ; 25cm), điểm C cách O là 7cm. Có bao nhiêu dây đi qua C có độ dài là một số nguyên xentimét?
-
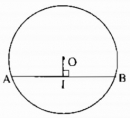
Câu 3.2 trang 161 Sách bài tập (SBT) Toán 9 lớp Tập 1
Cho đường tròn (O), điểm I nằm bên trong đường tròn ( I khác O). Dựng dây AB đi qua I và có độ dài ngắn nhất.

 Tải ngay
Tải ngay