CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM VỀ KHẢO SÁT HÀM SỐ

Bình chọn:

4.4 trên 124 phiếu

Bài 1.44 trang 35 Sách bài tập (SBT) Giải tích 12

Xác định m để đồ thị (Cm) của hàm số đã cho có ba điểm cực trị
Bài 1.45 trang 35 Sách bài tập (SBT) Giải tích 12

Khảo sát sự biến thiên và vẽ đồ thị của hàm số.
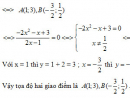
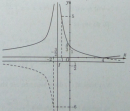
Bài 1.46 trang 36 Sách bài tập (SBT) Giải tích 12

Xác định tọa độ giao điểm của đồ thị (C) với đường thẳng y = x + 2.
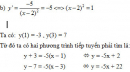
Bài 1.47 trang 36 Sách bài tập (SBT) Giải tích 12

Viết phương trình tiếp tuyến của đồ thị (C) , biết hệ số góc của tiếp tuyến bằng – 5.
Bài 1.48 trang 36 Sách bài tập (SBT) Giải tích 12

Xét tính đơn điệu của hàm số.
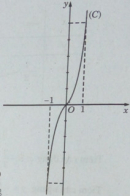
Bài 1.49 trang 36 Sách bài tập (SBT) Giải tích 12

Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số ứng với m = 1
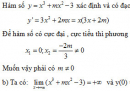
Bài 1.50 trang 37 Sách bài tập (SBT) Giải tích 12

Xác định m để hàm số (1) luôn luôn có cực đại, cực tiểu.
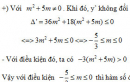
Bài 1.51 trang 37 Sách bài tập (SBT) Giải tích 12

Xác định m để hàm số đơn điệu trên R. Khi đó, hàm số đồng biến hay nghịch biến? Tại sao?
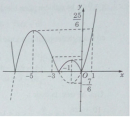
Bài 1.52 trang 37 Sách bài tập (SBT) Giải tích 12

Xác định a để đồ thị của hàm số cắt trục hoành tại ba điểm phân biệt.
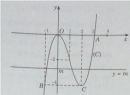
Bài 1.53 trang 37 Sách bài tập (SBT) Giải tích 12

Khảo sát sự biến thiên và vẽ đồ thị của hàm số đã cho.

Bài 1.54 trang 38 Sách bài tập (SBT) Giải tích 12

Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho
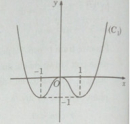
Bài 1.55 trang 38 Sách bài tập (SBT) Giải tích 12

Khảo sát sự biến thiên và vẽ đồ thị của hàm số khi m = 1
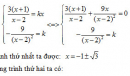
Bài 1.56 trang 38 Sách bài tập (SBT) Giải tích 12

Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.
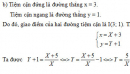
Bài 1.57 trang 38 Sách bài tập (SBT) Giải tích 12

Chứng minh rằng giao điểm I của hai tiệm cận của (C) là tâm đối xứng của (C).
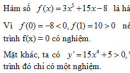
Bài 1.58 trang 38 Sách bài tập (SBT) Giải tích 12

Chứng minh rằng phương trình: 3x5 + 15x – 8 = 0 chỉ có một nghiệm thực.
Bài tập trắc nghiệm trang 38, 39 Sách bài tập (SBT) Giải tích 12

Hàm số dạng này có một điểm cực đại tại x = 0 và đồng biến trên khoảng (-∞; b) với b ≤ 0. Vậy hàm số đồng biến trên khoảng (-∞; 0).