Các mục con
-

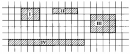
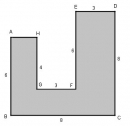
Câu 19 trang 158 Sách bài tập (SBT) Toán 8 tập 1
Tính diện tích các hình trên hình 182 (mỗi ô vuông là một đơn vị diện tích ).
-
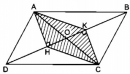
Câu 21 trang 158 Sách bài tập (SBT) Toán 8 tập 1
Chứng minh rằng hai đa giác ABCH và ADCK có cùng diện tích.
-
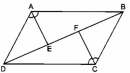
Câu 22 trang 158 Sách bài tập (SBT) Toán 8 tập 1
Chứng minh rằng hai hình ABCFE và ADCFE có cùng diện tích.
-
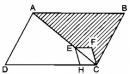
Câu 23 trang 158 Sách bài tập (SBT) Toán 8 tập 1
Chứng minh rằng đa giác AEHD và hình ABCFE có cùng diện tích.
-
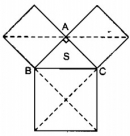
Câu 24 trang 159 Sách bài tập (SBT) Toán 8 tập 1
Chứng minh rằng tổng diện tích của hai hình vuông dựng trên hai cạnh góc vuông bằng diện tích của hình vuông dựng trên cạnh huyền(không sử dụng định lý Py-ta-go)
-
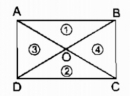
Câu 25 trang 159 Sách bài tập (SBT) Toán 8 tập 1
Hai đường chéo của hình chữ nhật chia hình chữ nhật thành bốn tam giác. Diện tích của các tam giác đó có bằng nhau không ? Vì sao ?
-
Câu 2.1 trang 159 Sách bài tập (SBT) Toán 8 tập 1
Để có thể lát kín nền đó cần bao nhiêu viên gạch có hình vuông, với cạnh là 33,33cm ?
-
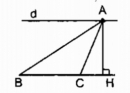
Câu 26 trang 159 Sách bài tập (SBT) Toán 8 tập 1
Cho tam giác ABC có đáy BC cố định và đỉnh A di động trên một đường thẳng d cố định song song với đường thẳng BC. Chứng minh rằng tam giác ABC luôn có diện tích không đổi.
-
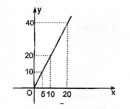
Câu 27 trang 159 Sách bài tập (SBT) Toán 8 tập 1
Tam giác ABC có đáy BC cố định và dài 4cm. Đỉnh A di chuyển trên đường thẳng d (d ⊥ BC). Gọi H là chân đường cao hạ từ đỉnh A xuống đường thẳng BC.
-
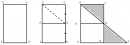
Câu 3.1 trang 160 Sách bài tập (SBT) Toán 8 tập 1-
a. Có thể dùng kéo cắt hai lần và chỉ cắt theo đường thẳng chia một tam giác (thường) thành ba mảnh để ghép lại được một hình chữ nhật hay không ?
-
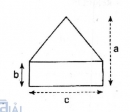
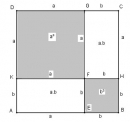
Câu 28 trang 160 Sách bài tập (SBT) Toán 8 tập 1
Tính diện tích của hình 186 theo các kích thước đã cho trên hình (a, b, c có cùng đơn vị đo).
-
Câu 29 trang 160 Sách bài tập (SBT) Toán 8 tập 1
Hai cạnh của một tam giác có độ dài là 5cm và 6cm. Hỏi diện tích của tam giác đó có thể lấy giá trị nào trong các giá trị sau:
-
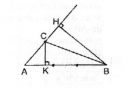
Câu 30 trang 160 Sách bài tập (SBT) Toán 8 tập 1
Cho tam giác ABC, biết AB = 3AC. Tính tỉ số hai đường cao xuất phát từ các đỉnh B và C.
-
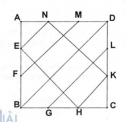
Câu 31 trang 160 Sách bài tập (SBT) Toán 8 tập 1
Tính diện tích của ngũ giác AEPSN và của tứ giác PQRS, biết AB = 6cm.
-
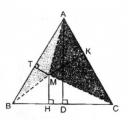
Câu 3.2 trang 161 Sách bài tập (SBT) Toán 8 tập 1
Cho tam giác đều ABC và điểm M bất kì nằm trong tam giác đó. Đường thẳng đi qua điểm M và vuông góc với BC tại điểm H. Đường thẳng đi qua điểm M và vuông góc với CA tại điểm K. Đường thẳng đi qua điểm M và vuông góc với AB tại điểm T.
-
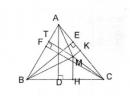
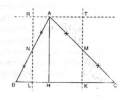
Câu 3.3 trang 161 Sách bài tập (SBT) Toán 8 tập 1
Cho hai tam giác ABC và DBC. Kẻ đường cao AH của tam giác ABC. Kẻ đường cao DK của tam giác DBC. Gọi S là diện tích của tam giác ABC. Gọi S’ là diện tích của tam giác DBC.

 Tải ngay
Tải ngay