Các mục con
- Bài 1. Định lí Ta-lét trong tam giác
- Bài 2. Định lí đảo và hệ quả của định lí Ta-lét
- Bài 3. Tính chất đường phân giác của tam giác
- Bài 4. Khái niệm hai tam giác đồng dạng
- Bài 5. Trường hợp đồng dạng thứ nhất (c.c.c)
- Bài 6. Trường hợp đồng dạng thứ hai (c.g.c)
- Bài 7. Trường hợp đồng dạng thứ ba (g.g)
- Bài 8. Các trường hợp đồng dạng của tam giác vuông
- Ôn tập chương III - Tam giác đồng dạng
-
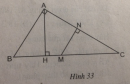
Câu 47 trang 95 Sách bài tập (SBT) Toán 8 tập 2
Trên hình 33 hãy chỉ ra các tam giác đồng dạng. Viết các cặp tam giác đồng dạng theo thứ tự các đỉnh tương ứng và giải thích vì sao chúng đồng dạng.
-
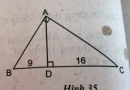
Câu 49 trang 96 Sách bài tập (SBT) Toán 8 tập 2
Đường cao của một tam giác vuông xuất phát từ đỉnh góc vuông chia cạnh huyền thành hai đoạn thẳng có độ dài là 9cm và 16cm. Tính độ dài các cạnh của tam giác vuông đó (h.35)
-
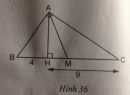
Câu 50 trang 96 Sách bài tập (SBT) Toán 8 tập 2
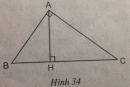
Tính diện tích tam giác AMH, biết rằng BH = 4cm, CH = 9cm.
-
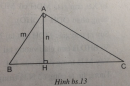
Câu 8.2 trang 96 Sách bài tập (SBT) Toán 8 tập 2
Hãy tính độ dài các cạnh còn lại của tam giác (chính xác đến hai chữ số thập phân)
-
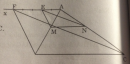
Câu 51 trang 97 Sách bài tập (SBT) Toán 8 tập 2
Vẽ đoạn thẳng MN. Hỏi rằng hai đường thẳng MN và BC có song song với nhau không ? Vì sao ?
-
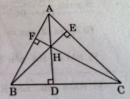
Câu 55 trang 98 Sách bài tập (SBT) Toán 8 tập 2
Tam giác ABC có ba đường cao AD, BE, CF đồng quy tại H. Chứng minh rằng AH.DH = BH.EH = CH.FH
-
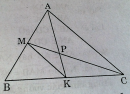
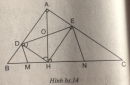
Câu 56 trang 98 Sách bài tập (SBT) Toán 8 tập 2
Chứng minh rằng AK và CM là các trung tuyến của tam giác ABC.
-
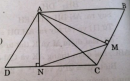
Câu 57 trang 98 Sách bài tập (SBT) Toán 8 tập 2
Chứng minh rằng tam giác MAN đồng dạng với tam giác ABC.
-
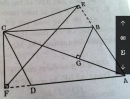
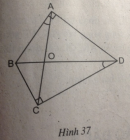
Câu 58 trang 98 Sách bài tập (SBT) Toán 8 tập 2
Giả sử AC là đường chéo lớn của hình bình hành ABCD. Từ C, vẽ đường vuông góc CE với đường thẳng AB, đường vuông góc CF với đường thẳng AD (E,F thuộc phần kéo dài của các cạnh AB và AD)
-
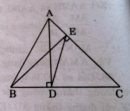
Câu 59 trang 98 Sách bài tập (SBT) Toán 8 tập 2
Chứng minh hai tam giác DEC và ABC là hai tam giác đồng dạng.
-
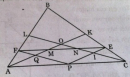
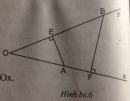
Câu 60 trang 98 Sách bài tập (SBT) Toán 8 tập 2
Chứng minh rằng các đoạn thẳng FM, MN, NE bằng nhau.

 Tải ngay
Tải ngay