Các mục con
-
Bài 3.41 trang 131 sách bài tập (SBT) – Hình học 12
Cho điểm M(1; -1; 2) và mặt phẳng : 2x – y + 2z + 12 = 0
-
Bài 3.42 trang 131 sách bài tập (SBT) – Hình học 12
Lập phương trình đường vuông góc chung của d và d’.
-
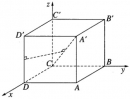
Bài 3.43 trang 131 sách bài tập (SBT) – Hình học 12
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Bằng phương pháp tọa độ hãy tính khoảng cách giữa hai đường thẳng CA’ và DD’.
-
Bài 3.44 trang 131 sách bài tập (SBT) – Hình học 12
Cho mặt phẳng : 2x + y +z – 1 = 0 và đường thẳng d: Gọi M là giao điểm của d và , hãy viết phương trình của đường thẳng đi qua M vuông góc với d và nằm trong
-
Bài 3.46 trang 131 sách bài tập (SBT) – Hình học 12
Lập phương trình mặt phẳng (P) đi qua điểm M(1; -3; 2) và vuông góc với đường thẳng d
-
Bài 3.47 trang 131 sách bài tập (SBT) – Hình học 12
Lập phương trình mặt phẳng (P) đi qua điểm M(1; -3; 2) và song song với mặt phẳng (Q): x – z = 0.
-
Bài 3.48 trang 131 sách bài tập (SBT) – Hình học 12
Lập phương trình mặt phẳng (P) đi qua ba điểm A(-1; -3; 2), B(-2; 1; 1) và C(0; 1; -1).
-
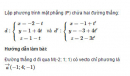
Bài 3.49 trang 132 sách bài tập (SBT) – Hình học 12
Lập phương trình mặt phẳng (P) chứa hai đường thẳng:
-
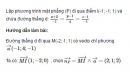
Bài 3.50 trang 132 sách bài tập (SBT) – Hình học 12
Lập phương trình mặt phẳng (P) đi qua điểm I(-1; -1; 1) và chứa đường thẳng d:
-
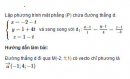
Bài 3.51 trang 132 sách bài tập (SBT) – Hình học 12
Lập phương trình mặt phẳng (P) chứa đường thẳng d: và song song với d1:
-
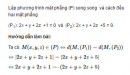
Bài 3.52 trang 132 sách bài tập (SBT) – Hình học 12
Lập phương trình mặt phẳng (P) song song và cách đều hai mặt phẳng (P1): 2x + y + 2z +1 = 0 và (P2): 2x + y + 2z +5 = 0.
-
Bài 3.53 trang 132 sách bài tập (SBT) – Hình học 12
Cho hai mặt phẳng: (P1): 2x + y + 2z +1 = 0 và (P2): 4x – 2y – 4z + 7 = 0. Lập phương trình mặt phẳng sao cho khoảng cách từ mỗi điểm của nó đến (P1) và (P2) là bằng nhau.
-
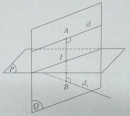
Bài 3.54 trang 132 sách bài tập (SBT) – Hình học 12
Cho hai đường thẳng d: và d1: Lập phương trình mặt phẳng (P) sao cho khoảng cách từ d và d1 đến (P) là bằng nhau.
-

Bài 3.55 trang 132 sách bài tập (SBT) – Hình học 12
Lập phương trình mặt phẳng (P) đi qua điểm M(1; -3; 2) và vuông góc với hai mặt phẳng (Q): 2x – y +3z + 1 = 0 và (R): x – 2y – z + 8 = 0
-
Bài 3.56 trang 132 sách bài tập (SBT) – Hình học 12
Lập phương trình tham số của đường thẳng d đi qua hai điểm phân biệt M0(x0 ;y0; z0) và M1(x1, y1, z1)
-

Bài 3.57 trang 132 sách bài tập (SBT) – Hình học 12
Lập phương trình tham số của đường thẳng d đi qua điểm M0(x0, y0, z0) và vuông góc với mặt phẳng (P): Ax + By + Cz + D = 0.
-
Bài 3.58 trang 132 sách bài tập (SBT) – Hình học 12
Lập phương trình tham số của đường thẳng d đi qua điểm M0(x0, y0, z0) và song song với hai mặt phẳng cắt nhau (P) Ax + By + Cz + D = 0 và (Q): A’x + B’y + C’z + D’ = 0
-

Bài 3.59 trang 133 sách bài tập (SBT) – Hình học 12
Cho mặt phẳng (P) : x + 2y – 2z + 3 = 0 và đường thẳng d: Lập phương trình đường thẳng d’ là hình chiếu vuông góc của d lên mặt phẳng (P).
-
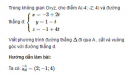
Bài 3.60 trang 133 sách bài tập (SBT) – Hình học 12
Trong không gian Oxyz, cho điểm A(-4; -2; 4) và đường thẳng d: Viết phương trình đường thẳng đi qua A , cắt và vuông góc với đường thẳng d.

 Tải ngay
Tải ngay