Các mục con
- Bài 6. Đối xứng trục
- Bài 7. Hình bình hành
- Bài 8. Đối xứng tâm
- Bài 9. Hình chữ nhật
- Bài 10. Đường thẳng song song với một đường thẳng cho trước
- Bài 11. Hình thoi
- Bài 12. Hình vuông
- Bài tập ôn chương I - Tứ giác
- Bài 1. Tứ giác
- Bài 2. Hình thang
- Bài 3. Hình thang cân
- Bài 4. Đường trung bình của tam giác, của hình thang
- Bài 5. Dựng hình bằng thước và com pa. Dựng hình thang
-
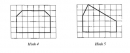
Câu 68 trang 87 Sách bài tập (SBT) Toán 8 tập 1
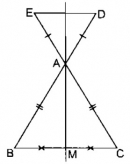
Trong các hình nét đậm vẽ trên giấy kẻ ô vuông ở hình 4, hình 5, hình nào có trục đối xứng ?
-
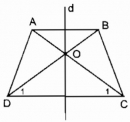
Câu 71 trang 88 Sách bài tập (SBT) Toán 8 tập 1
Chứng minh rằng giao điểm hai đường chéo của hình thang cân nằm trên trục đối xứng của hình thang cân.
-
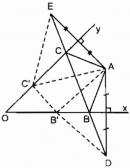
Câu 72 trang 88 Sách bài tập (SBT) Toán 8 tập 1
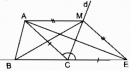
Cho góc nhọn xOy, điểm A nằm trong góc đó. Dựng điểm B thuộc tia Ox, điểm C thuộc tia Oy sao cho tam giác ABC có chu vi nhỏ nhất.
-

Câu 6.1 trang 88 Sách bài tập (SBT) Toán 8 tập 1
Hãy nối mỗi cột của ô bên trái với một ô của cột bên phải để được khẳng định đúng.
-
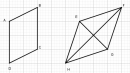
Câu 73 trang 89 Sách bài tập (SBT) Toán 8 tập 1
Các tứ giác ABCD, EFGH vẽ trên giấy kẻ ô vuông ở hình 7 có là hình bình hành không ?
-
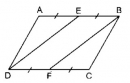
Câu 74 trang 89 Sách bài tập (SBT) Toán 8 tập 1
Cho hình bình hành ABCD. Gọi E là trung điểm của AB, F là trung điểm của CD. Chứng minh rằng DE = BF.
-
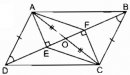
Câu 76 trang 89 Sách bài tập (SBT) Toán 8 tập 1
Trên hình 8, cho ABCD là hình bình hành. Chứng minh rằng AECF là hình bình hành.
-
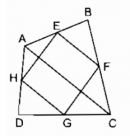
Câu 77 trang 89 Sách bài tập (SBT) Toán 8 tập 1
Tứ giác ABCD có E, F, G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì ? Vì sao ?
-
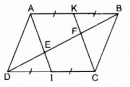
Câu 78 trang 89 Sách bài tập (SBT) Toán 8 tập 1
Cho hình bình hành ABCD. Gọi I, K theo thứ tự là trung điểm của CD , AB. Đường chéo BD cắt AI, CK theo thứ tự ở E, F. Chứng minh rằng DE = EF = FB.
-
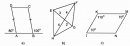
Câu 80 trang 89 Sách bài tập (SBT) Toán 8 tập 1
Trong các tứ giác trên hình 9, tứ giác nào là hình bình hành ?
-
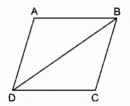
Câu 81 trang 90 Sách bài tập (SBT) Toán 8 tập 1
Chu vi hình bình hành ABCD bằng 10cm, chu vi tam giác ABD bằng 9cm. Tính độ dài BD.
-
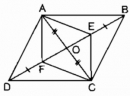
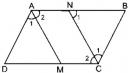
Câu 82 trang 90 Sách bài tập (SBT) Toán 8 tập 1
Trên hình 10, cho ABCD là hình bình hành. Chứng minh rằng AE // CF.
-
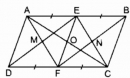
Câu 83 trang 90 Sách bài tập (SBT) Toán 8 tập 1
Chứng minh rằng : a. EMFN là hình bình hành. b. Các đường thẳng AC, EF, MN đồng quy.
-
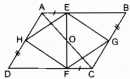
Câu 84 trang 90 Sách bài tập (SBT) Toán 8 tập 1
Trên hình 11, cho ABCD là hình bình hành. Chứng minh rằng:
-
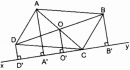
Câu 85 trang 90 Sách bài tập (SBT) Toán 8 tập 1
Cho hình bình hành ABCD. Qua C kẻ đường thẳng xy chỉ có một điểm chung C với hình bình hành. Gọi AA’, BB’, DD’ là các đường vuông góc kẻ từ A, B, D đến đường thẳng xy. Chứng ming rằng AA’ = BB’ + DD’.

 Tải ngay
Tải ngay