CHƯƠNG I. TỨ GIÁC | Sachbaitap.com

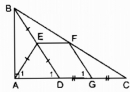
Câu 120 trang 95 Sách bài tập (SBT) Toán 8 tập 1

Cho tam giác ABC vuông tại A, điểm D thuộc cạnh AC. Gọi E, F, G theo thứ tự là trung điểm của BD, BC, DC. Chứng minh rằng tứ giác AEFG là hình thang cân.

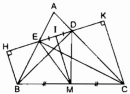
Câu 121 trang 95 Sách bài tập (SBT) Toán 8 tập 1

Cho tam giác nhọn ABC, các đường cao BD, CE. Gọi H, K theo thứ tự là chân các đường vuông góc kẻ từ B, C đến đường thẳng DE. Chứng minh rằng EH = DH

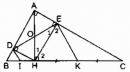
Câu 122 trang 95 Sách bài tập (SBT) Toán 8 tập 1

Cho tam giác ABC vuông tại A, đường cao AH. Gọi D, E theo thứ tự là chân các đường vuông góc kẻ từ H đến AB, AC.

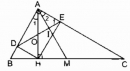
Câu 123 trang 95 Sách bài tập (SBT) Toán 8 tập 1

Cho tam giác ABC vuông tại A, đường cao AH, đường trung tuyến AM.

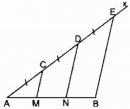
Câu 124 trang 95 Sách bài tập (SBT) Toán 8 tập 1

Chứng minh rằng đoạn thẳng AB bị chia ra ba phần bằng nhau.

Câu 9.1 trang 95 Sách bài tập (SBT) Toán 8 tập 1

Một hình chữ nhật có hai cạnh kề bằng nhau 4cm và 6cm. Độ dài đường chéo của hình chữ nhật đó bằng bao nhiêu xentimét ?

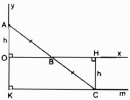
Câu 125 trang 95 Sách bài tập (SBT) Toán 8 tập 1

Cho góc vuông xOy, điểm A trên tia Oy. Điểm B di chuyển trên tia Ox. Gọi C là điểm đối xứng với A qua B. Điểm C di chuyển trên đường nào ?

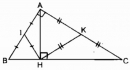
Câu 9.2 trang 95 Sách bài tập (SBT) Toán 8 tập 1

Cho tam giác ABC vuông tại A, đường cao AH. Gọi I, K theo thứ tự là trung điểm của AB, AC. Tính số đo góc IHK.

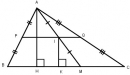
Câu 126 trang 96 Sách bài tập (SBT) Toán 8 tập 1

Cho tam giác ABC, điểm M di chuyển trên cạnh BC. Gọi I là trung điểm của AM. Điểm I di chuyển trên đường nào ?

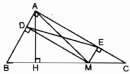
Câu 127 trang 96 Sách bài tập (SBT) Toán 8 tập 1

a. So sánh các độ dài AM, DE. b. Tìm vị trí của điểm M trên cạnh BC để DE có độ dài nhỏ nhất.

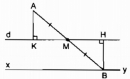
Câu 128 trang 96 Sách bài tập (SBT) Toán 8 tập 1

Cho điểm A nằm ngoài đường thẳng d. Điểm M di chuyển trên đường thẳng d. Gọi B là điểm đối xứng với A qua M. Điểm B di chuyển trên đường nào ?

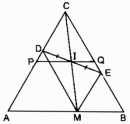
Câu 129 trang 96 Sách bài tập (SBT) Toán 8 tập 1

Cho đoạn thẳng AB, điểm M di chuyển trên đoạn thẳng ấy. Vẽ về một phía của AB các tam giác đều AMD, BME. Trung điểm I của DE di chuyển trên đường nào ?

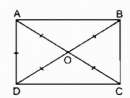
Câu 130 trang 96 Sách bài tập (SBT) Toán 8 tập 1

Hình chữ nhật ABCD có cạnh AD bằng nửa đường chéo AC. Tính góc nhọn tạo bởi hai đường chéo.

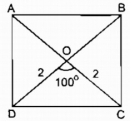
Câu 131 trang 96 Sách bài tập (SBT) Toán 8 tập 1

Dựng hình chữ nhật ABCD, biết đường chéo AC = 4cm, góc tạo bởi hai đường chéo bằng 100°.

Câu 10.1 trang 96 Sách bài tập (SBT) Toán 8 tập 1

Hãy chọn phương án đúng.

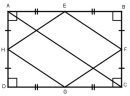
Câu 132 trang 96 Sách bài tập (SBT) Toán 8 tập 1

Chứng minh rằng trung điểm bốn cạnh của một hình chữ nhật là đỉnh của một hình thoi.

Câu 10.2 trang 96 Sách bài tập (SBT) Toán 8 tập 1

Điểm M chuyển động trên đường nào ?

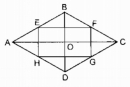
Câu 133 trang 96 Sách bài tập (SBT) Toán 8 tập 1

Chứng minh rằng trung điểm các cạnh của một hình thoi là đỉnh của một hình chữ nhật.

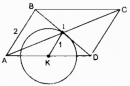
Câu 10.3 trang 96 Sách bài tập (SBT) Toán 8 tập 1

Xét các hình bình hành ABCD có cạnh AD cố định, cạnh AB = 2cm. Gọi I là giao điểm của AC và BD. Điểm I chuyển động trên đường nào ?

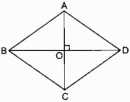
Câu 134 trang 97 Sách bài tập (SBT) Toán 8 tập 1

Chứng minh rằng trong hình thoi: a. Giao điểm của hai đường chéo là tâm đối xứng của hình thoi b. Hai đường chéo là hai trục đối xứng của hình thoi.

Các mục con